|
4.2 Observer-Hessenberg Forms
The duals of the controller-Hessenberg forms are the observer-Hessenberg forms. Given the  state matrix A and the state matrix A and the  output matrix output matrix  , there exists an orthogonal matrix T, such that , there exists an orthogonal matrix T, such that


where each  is an is an  matrix, the matrix matrix, the matrix  is is  and and  is the transpose of is the transpose of  . The rectangular superdiagonal block matrices . The rectangular superdiagonal block matrices  , ,  , ..., , ..., 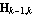 are lower triangular and the matrix are lower triangular and the matrix  is also rectangular and lower triangular. The matrices is also rectangular and lower triangular. The matrices  and and  are transformed to are transformed to  and and  as as  and and . The pair ( . The pair ( , ,  ) is called the lower observer-Hessenberg form of the pair ( ) is called the lower observer-Hessenberg form of the pair ( , ,  ) or simply the observer-Hessenberg form. ) or simply the observer-Hessenberg form.
Note that in the single-input case,  is just a lower Hessenberg matrix and is just a lower Hessenberg matrix and  is a multiple of is a multiple of  . .
The superdiagonal blocks  , ,  , ..., , ...,  in the matrix in the matrix  are of particular importance: the state-space system is observable if and only if they all have full rank, in which case the observer-Hessenberg form is called unreduced. When the system is unobservable, the superdiagonal blocks are of particular importance: the state-space system is observable if and only if they all have full rank, in which case the observer-Hessenberg form is called unreduced. When the system is unobservable, the superdiagonal blocks  have full rank and the last block have full rank and the last block  is zero. is zero.
The upper observer-Hessenberg form is given by

 
where  is a is a  rectangular upper triangular matrix. rectangular upper triangular matrix.
Both the lower and upper observer-Hessenberg forms are constructed by duality of the staircase algorithm for the controller-Hessenberg forms. By default, lower observer-Hessenberg form is used.




The observer-Hessenberg realizations.
Pivoting, obtained with the option value Pivoting True, improves the computational accuracy. Note that the triangular structure of superdiagonal blocks may be lost when pivoting is used. True, improves the computational accuracy. Note that the triangular structure of superdiagonal blocks may be lost when pivoting is used.
Make sure the application is loaded.
In[1]:=
Load the collection of state-space systems.
In[2]:=
Consider the same drum boiler system in the previous example.
In[3]:=
Out[3]=
This is the lower observer-Hessenberg form of the drum boiler system.
In[4]:=
Out[4]//NumberForm=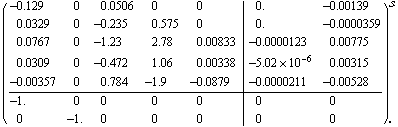
This is the upper observer-Hessenberg form of the drum boiler system.
In[5]:=
Out[5]//NumberForm=
|