|
Pendulum Example for MechanicalSystems Kinematics and Dynamicsby Robert Beretta
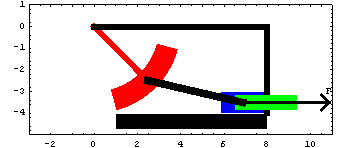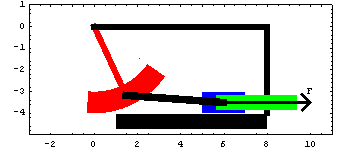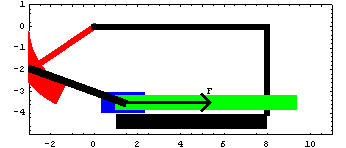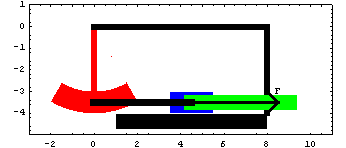
Pendulum AnimationDiscussionPendulum FunctionThis sample notebook analyzes the motion of a pendulum that is attached to a sliding mass and a spring. This mechanism is used to demonstrate the use of the forcing functions provided by MechanicalSystems.
The pendulum swings on a pivot attached to the ground body. The input to the model is a driving constraint causing the pendulum to swing. The pendulum is attached to the slider by a connecting rod. Pendulum ModelThe pendulum-slider mechanism consists of four bodies.
1. Ground (black)
2. Pendulum (red)
3. Slider (blue)
4. Connecting rod (black) Kinematic ModelPreparationThe Modeler2D package is loaded into Mathematica with the Needs command. SetSymbols is used to change the way that Modeler2D represents angular orientation, velocity, and acceleration. The Method -> Angular setting is the default, but this could be changed here to Method -> Euler. The following symbols are used to reference each of the bodies in the pendulum mechanism throughout the analysis. Body DefinitionsGroundThree points are defined on the ground body (body 1).
P1. A point at the left end of the slider track.
P2. A point at the right end of the slider track.
P3. The attachment point of the spring. PendulumOne point is defined on the pendulum (body 2) as well as its inertia properties.
P1. The attachment point of the connecting rod. SliderTwo points are defined on the slider (body 3) as well as its inertia properties.
P1. A point at the left bottom surface of the slider.
P2. A point at the right bottom surface of the slider. Connecting rodTwo points are used on the connecting rod (body 4) as well as its inertia properties.
P0. The left attachment point of the connecting rod, at the local origin.
P1. The right attachment point of the connecting rod. Build bodiesThe data contained in each of the body objects is entered into the current model with the Modeler2D SetBodies command. Constraint DefinitionsFive constraints, including one driving constraint, are required to model the pendulum mechanism. Pendulum constraints 1. A driving constraint to rotate the pendulum.
2. A revolute constraint to place the axis of the pendulum. The parameter drfreq is the frequency of the driver, in hertz. The frequency is set with SetParameters so that it remains variable throughout the notebook. Connecting rod and slider constraints 3. A translational joint.
4. A revolute joint between the connecting rod and the pendulum.
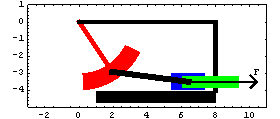
5. A revolute joint between the connecting rod and the slider. The data contained in each of the constraint objects is entered into the current model with the Modeler2D SetConstraints command. Running the ModelCheckSystem tests for certain modeling errors. A return value of True is OK. SolveMech[t] runs the current model at time t and returns a list of rules containing the X, Y, and  coordinates of each body. coordinates of each body. GraphicsMechanism Image
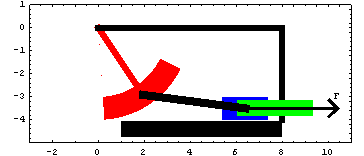
AnimationThe following input generates the series of 14 graphics in the animation cell at the beginning of this notebook. Applying ForcesModeler2D defines all of the necessary functions for static and dynamic force analysis. Mech allows forces to be applied to kinematic models and then solves for the reactions to those forces at each of the mechanism's joints. Load DefinitionsForce objects are built up in much the same way as constraint objects are built. Four force objects, Force, Moment, Load, and Gravity, are available. To model a spring between the slider and the ground, Force is used to apply a force to the slider, the magnitude of which is a function of the distance between the slider and the ground. The symbol springforce needs to be a function of the length of the spring. This function can be generated with the Distance function. The extension spring is to have a spring constant of 12. The loads are then passed to SetLoads, just as the constraints are passed to SetConstraints. Running the Loaded ModelNow that loads have been defined, the Solution -> Static option is used to solve for the reaction forces. The solution rules returned with Solution->Static contain the complete location solution returned by Solution->Location and the Lagrange multiplier solution. The symbols 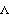 1, 1, 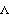 2, ... , are the Lagrange multipliers, or generalized forces, associated with each constraint equation. 2, ... , are the Lagrange multipliers, or generalized forces, associated with each constraint equation. ReactionsThe Lagrange multipliers are not directly very useful; they are transformed into useful output with the Reaction function. The torque required at the pivot to hold the pendulum in the current position, against the force of the spring, is the reaction of the pendulum to constraint 1, calculated about the pivot point of the pendulum. The list returned by Reaction, 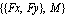 contains the force vector and moment applied to the specified body by the specified constraint (positive moments are counterclockwise). Thus, it takes 82.8 units of clockwise torque to hold the pendulum where it is. contains the force vector and moment applied to the specified body by the specified constraint (positive moments are counterclockwise). Thus, it takes 82.8 units of clockwise torque to hold the pendulum where it is.
The Fx and Fy forces returned are zero not because the force at the pivot is zero, but because the force at the pivot due to constraint 1 is zero. Constraint 1 is a RotationLock1 constraint that does not enforce the X or Y position, so it can have no X or Y reaction.
The X-Y reaction at the pivot is due to constraint 2. Note that the point about which to calculate the moments was not specified explicitly. The default is to calculate moments about the origin of the specified body.
The X-Y reaction at the pivot is equal and opposite to the force applied to the pendulum by the connecting rod, constraint 4. This, of course, is equal and opposite to the force applied to the slider by the connecting rod. The translational joint that constrains the slider supports the vertical component of the force in the connecting rod. In all cases, the sum of all reaction forces plus all applied forces on a particular body is zero. FindTime with Reaction ForcesFindTime[equation] can be used with an equation that involves Lagrange multipliers, which usually results from specifying the magnitude of a constraint reaction force. The following example uses FindTime to find the time at which the pivot reaction torque is -50. Other Load TypesFrictionFriction forces are modeled simply by applying forces whose magnitudes are functions of other forces. Friction between the slider and the ground is a function of the magnitude of the reaction force at the translational joint, constraint 3. Note that the friction force in this case is always in the -X direction--it must be reversed to model the slider going the other way. The reaction at rotational driver is slightly reduced. GravityGravitational forces are applied to the model with Gravity. The force due to friction is now great enough to more than completely counter the force due to the spring, due to the increase in normal force on the slider. The reaction at the rotational driver is much less. Velocity Dependent ForcesIf loads that are functions of velocity are present in the model, Solution -> Kinematic is used instead of Solution -> Static. Kinematic simply runs the velocity solution block before the load solution block and applies the velocity rules if velocity terms appear in the applied loads. If there are no velocity terms in the generalized forces, Kinematic produces the same results as Static.
We can add a damper to the slider that applies a force counter to the velocity of the slider. At the same time, we can modify the friction force so that its sign is dependent on the velocity of the slider. This solves for the location and velocity of each body, as well as the generalized forces. The forces due to friction and the viscous damper now far outweigh the forces due to the spring. FindTime can also be used with velocity dependent forces. This shows that the specified condition has been satisfied. Inverse DynamicsIf inertial forces are to be included in the model, Solution->Dynamic must be used instead of Solution->Kinematic or Static. The Dynamic setting runs the velocity and acceleration solution blocks and then calculates the inertial forces that result from the linear and angular acceleration of each body. In order for the dynamic forces to be nonzero, mass and inertia properties must be specified with SetBodies.
Since masses have already been specified for the pendulum and slider, simply running SolveMech with the Solution->Dynamic option, without changing any forces, calculates the dynamic forces in the model. The dynamic forces are rather large! If the speed of the pendulum is reduced, the inertial forces will drop. The model is slowed by giving the Sin function in the driver a lower frequency. Note that T = 0.4 is an equivalent position to T = 0.1, with the old driver frequency.
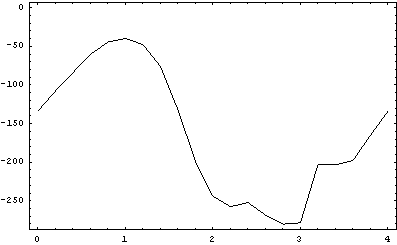
Force PlotsThis generates a list of 21 solutions. Here is a plot of the torque required to drive the pendulum at 0.25 hertz.
EquilibriumStatic Forces Define a load object An extension spring is added to the model, attached between the slider and the ground. The spring has a spring constant of 12 and has zero force when it is 2 units long. This build the generalized force vector and applies it to the model. Use the Solution option to cause SolveMech to return the current Lagrange multiplier solution. Reaction Forces Here a function is defined that returns the torque required to drive the pendulum. This outputs the pendulum reaction torque and the pendulum angle. If we rotate the pendulum farther counterclockwise, the torque required at the pendulum pivot approaches and passes through zero. Equilibrium PositionIf there were no constraint on the rotational position of the pivot, there would exist some equilibrium condition where the mechanism would come to rest. This position is found with the SolveFree solution block.
SetFree[] builds the system of equations necessary to find the equilibrium position of the mechanism. SolveFree solves those equations. SetFree is used to drop the driving constraint (constraint 1) since we know that an equilibrium position exists for the mechanism with the pendulum driver released, somewhere around T < 0.2. As expected, the equilibrium position puts  2 between the two values found at T = 0.1 and T = 0.2. 2 between the two values found at T = 0.1 and T = 0.2. More ForcesSince there is only one force in the current model, the equilibrium position is when that force, and hence all the reaction forces, is zero.
We can add gravitational forces so that the equilibrium position is nontrivial. The reaction at rotational driver is much increased at T = 0.1. Again, an equilibrium position must exist between T = 0.01 and T = 0.1. Again, the equilibrium position puts  2 between the two values found at T = 0.01 and T = 0.1. 2 between the two values found at T = 0.01 and T = 0.1.
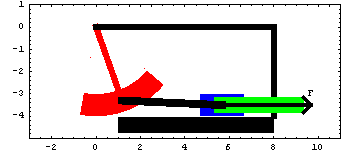
Equilibrium VelocityIf forces are included in the current model that are functions of velocity, then those forces will be set to zero when seeking an equilibrium position, because by definition all velocities are zero at an equilibrium position. But another condition can exist for a model with velocity dependent forces--the equilibrium velocity.
If a massless model with velocity-dependent forces (that is not completely constrained) is placed in some initial position and released, it instantaneously achieves its equilibrium velocity and then moves in a controlled manner. Every valid position of the mechanism has an associated equilibrium velocity.
A key word in this is "massless". No accelerations are calculated for the equilibrium velocity, not even centripetal accelerations, such as those in a pendulum swinging at constant angular velocity. However, if the Gravity function is used to apply forces, the mass of each body is used to calculate the force, but the bodies still have no effective inertia or resistance to acceleration, just weight.
To demonstrate, a viscous damper is added alongside the spring to the pendulum-slider model. A large counterclockwise torque is required to drive the pendulum at T = 0.1. Because of the Sin[2  T] driver, T = 0.4 is the same position as T = 0.1, but going the other way. A small negative torque is required to drive the pendulum in this direction and speed, so it must be close to the equilibrium velocity. T] driver, T = 0.4 is the same position as T = 0.1, but going the other way. A small negative torque is required to drive the pendulum in this direction and speed, so it must be close to the equilibrium velocity. SetFree takes the Solution option to tell it what type of equilibrium it is looking for. When seeking an equilibrium velocity, an initial position must be passed to SolveFree. Initial positions are specified by a solution rule, such as that returned by SolveMech. The equilibrium velocity of the entire mechanism is slightly slower than the driven velocity, at T = 0.4. Equilibrium AccelerationIf a mechanism is not massless, then accelerations are not instantaneous, and the concept of equilibrium velocity is not generally relevant. What is relevant is the equilibrium acceleration.
In a real mechanism in which each body has finite mass, translational or angular accelerations result from any unbalanced forces on the bodies (F = ma). If each body, in a mechanism that is not completely constrained, is placed in a consistent initial position and given a consistent initial velocity, then the sum of the applied forces and the reaction forces on each body results in some acceleration, the equilibrium acceleration. Every combination of initial position and initial velocity of the mechanism has an associated equilibrium acceleration.
SetFree[dropcon, Solution->Dynamic] builds the equations needed to find the equilibrium acceleration. Exactly the same model is analyzed as was used previously for the equilibrium velocity. The only difference is that in seeking the equilibrium acceleration, the inertia of each body is considered.
A fairly large clockwise torque is required to decelerate the pendulum at T = 0.1. If constraint 1 were to be released, it seems that the slider acceleration would be much less negative, possibly positive if the spring force outweighs the friction and the lifting of the pendulum. Here the Solution option is used to tell SetFree to build dynamic equilibrium equations with constraint 1 dropped, so the model is not fully constrained. When seeking an equilibrium acceleration, the initial position and velocity must be passed to SolveFree. Initial conditions are specified by a solution rule, such as that returned by SolveMech with the Solution->Velocity option. The slider acceleration is still negative, but its magnitude is cut in half by the removal of the force applied by the pendulum rotational driver. End
|