CheckSystem
2D/3D• CheckSystem[] checks the current model for undefined variables or inconsistent constraint sets. CheckSystem returns True if all is well, False and an error message otherwise. • CheckSystem goes through the following procedure to test the current mechanism model:
1. Look for new dependencies on location variables or the time variable in the constraint equations. If the user introduces a symbol s into the model and then defines s to be a function of Mech location variables (such as s = X2 Y2) after SetConstraints is used to build the constraint equations, the model will fail because symbolic differentiation with respect to X2 and Y2 was not possible in SetConstraints.
2. Look for new dependencies on velocity, acceleration, or generalized force variables in the constraint equations. If the user introduces a symbol s into the model and then defines s to be a function of other Mech variables (such as s = X2d 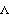 3), the model will fail. Systems that are kinematically dependent on higher-order terms are nonholonomic, and they are handled by SetPath, and systems that are kinematically dependent on generalized forces are underconstrained, and handled by SetFree. 3), the model will fail. Systems that are kinematically dependent on higher-order terms are nonholonomic, and they are handled by SetPath, and systems that are kinematically dependent on generalized forces are underconstrained, and handled by SetFree.
3. Look for new dependencies on any Mech system variables in the mass matrix. Such a dependency makes no physical sense.
4. Look for new dependencies on any Mech system variables in the applied load vector. Such dependencies are allowed, but they will confuse Mech's variable tracking if they appear after SetLoads is used to build the load vector. New dependencies on generalized force terms will cause the model to fail.
5. Look for undefined symbols that are not Mech system variables in any part of the model.
6. Check to see that the vector of constraint equations evaluates to a vector of numbers at the current values of the initial guesses. If this fails, examine the result of Constraints[All]/.LastSolve[] to see what the nonnumeric quantities are.
7. Check to see that the constraint derivatives are numeric at the current values of the initial guesses. This may fail because differentiation resulted in an indeterminate expression, even though the constraints were OK. Examine Jacobian, VelocityTerms, or AccelerationTerms for nonnumeric quantities.
8. Check to see that the total applied load vector evaluates to a vector of numbers at the current values of the initial guesses. If this fails, examine the result of Loads[All]/.LastSolve[] to see what the nonnumeric quantities are.
9. Check to see that the load vector derivatives are numeric at the current values of the initial guesses. This may fail because differentiation resulted in indeterminate expressions, or because the current guesses are unacceptable. Lagrange multiplier guesses should usually be nonzero.
10. Check that the constraint set shows some dependence on each of the dependent variables at the current initial guess state. If not, the model is singular. This may mean that the constraint set is inherently singular, or merely that better initial guesses are needed.
11. Check to see if the Jacobian of the current model is singular. If it is, Mech attempts to find the set of equations that are redundant and return their equation numbers. This may be due to poor initial guesses or inherently redundant constraints.
• See also: SetBodies. Further Examples Load the Modeler2D package and define a simple model. The help model initially has no errors.
Out[2]= | 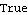 |
Here a variable var becomes dependent on a system variable after SetConstraints is run.
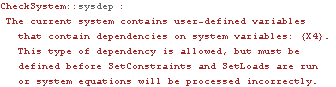
Out[7]= | 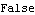 |
Here we replace the OriginLock2 constraint with another constraint that is redundant with respect to the existing constraint number 2, a RotationLock1 constraint.

Out[10]= | 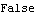 |
See HelpModel2D.
|