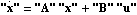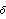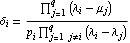Using the state-feedback spectral algorithm described in Patel and Munro (1982), the feedback matrix K that places the poles of a single-input system  at  {1},{2},...,n can be found as where vi is the ith row vector of the matrix V = W-1, W is the matrix of eigenvectors of A, and the  i are weighting factors calculated as  where q is the number of poles to be moved to new locations, the i are the open-loop system eigenvalues to be moved to these new locations, the  i are the desired closed-loop system eigenvalues, and the scalars pi are defined by the inner product pi=<vi,B>. It should be noted that even if the i and i are complex, the resulting state-feedback matrix K will be real. If the open-loop system has eigenvalues with multiplicity greater than 1, then the weighting factors calculated in Eq. (6.5) will be infinite. If this situation occurs, the matrix A of the original system is perturbed by an initial state feedback to separate any eigenvalues with multiplicity greater than one. In order to ensure that the resulting state-feedback matrix K is real, any complex open-loop system poles must be specified as complex conjugate pairs.
This algorithm gets its name from the use of the system reciprocal eigenvectors as projection operators used to select that part of the matrix spectrum to be operated on. The advantage of this algorithm over other dyadic pole assignment algorithms is that, in general, it is not necessary to specify all the resulting system closed-loop poles, only the q open-loop system poles to be moved and their new locations are specified. It therefore carries out fewer numerical calculations, in cases where there are no open-loop poles with multiplicity greater than one, than the other dyadic pole placement algorithms, and hence the results obtained tend to be more accurate. This can be important with high-order systems. The function StateFeedbackGains with the option Method  Spectral implements this algorithm. | StateFeedbackGains[system, {1, ..., k}, Method Spectral] |
| | find a state-feedback gain matrix that assigns the k (k < n) most unstable poles of the state-space system to the poles 1, ..., k, leaving the others unchanged |
| StateFeedbackGains[system, {{1 , ..., k} , {1 , ..., k}}, Method Spectral] |
|
| | reassign the poles 1, ..., k to the poles 1, ..., k, leaving the others unchanged |
Partial pole assignments. Make sure the application is loaded. Consider again the state-space model of the aircraft. | Out[3]= |  |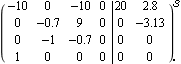
These are its open-loop system poles. | Out[5]= |  |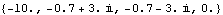
Here are the desired closed-loop system poles, when moving only the three slowest. This finds the state feedback using the spectral algorithm, finding the best combination of the inputs automatically. | Out[8]= |  |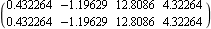
These are the resulting closed-loop system poles. | Out[10]= |  |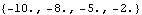
This is the infinity norm of the resulting state-feedback matrix. | Out[12]= |  |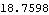
The norm of the feedback gains determined using the spectral algorithm is the same as that obtained using the mapping algorithm. This determines the state feedback needed to achieve the desired closed-loop poles, using the best input. | Out[14]= |  |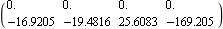
The infinity norm of this solution is bigger than that obtained using all the inputs. | Out[16]= |  |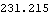
|
