|
2.1 Model PropertiesA discrete time series consists of a set of observations {x1, x2, ... , xt, ... } of some phenomenon, taken at equally spaced time intervals. (We assume that xt is real.) The main purpose of time series analysis is to understand the underlying mechanism that generates the observed data and, in turn, to forecast future values. We assume that the generating mechanism is probabilistic and that the observed series {x1, x2, ... , xt, ... } is a realization of a stochastic process {X1, X2, ... , Xt, ... }. Typically, the process is assumed to be stationary and described by a class of linear models called autoregressive moving average (ARMA) models. An ARMA model of orders p and q (ARMA(p, q)) is defined by where { i} i} and { i} i} are the coefficients of the autoregressive (AR) and moving average (MA) parts, respectively, and {Zt} is white noise with mean zero and variance  2 2. (We assume Zt is normally distributed.) Using the backward shift operator B defined by BjXt=Xt-j, the ARMA( p, q) model above can be written as where  (B)=1- (B)=1- 1B- 1B- 2B2-... - 2B2-... - pBp pBp and  (B)=1+ (B)=1+ 1B+ 1B+ 2B2+... + 2B2+... + qBq qBq. We assume that the polynomials  (x) (x) and  (x) (x) have no common zeros. When Xt is a vector, we have a multivariate or vector ARMA model; in this case, the AR and MA coefficients are matrices and the noise covariance is also a matrix denoted by  . When all the zeros of the polynomial  (x) (x) (or its determinant in the multivariate case) are outside the unit circle, the model is said to be stationary and the ARMA( p, q) model can be expanded formally as an MA( 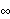 ) model ( Xt=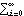  iZt-i iZt-i). Similarly, if the zeros of  (x) (x) are all outside the unit circle, the ARMA( p, q) model is said to be invertible and can be expanded as an AR( 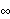 ) model. Autoregressive integrated moving average (ARIMA) models are used to model a special class of nonstationary series. An ARIMA(p, d, q) (d non-negative integer) model is defined by Seasonal models are used to incorporate cyclic components in models. A class of commonly encountered seasonal models is that of seasonal ARIMA (SARIMA) models. A SARIMA( p, d, q)( P, D, Q) s model ( d and D are non-negative integers and s is the period) is defined by where 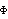 (x) (x) and 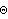 (x) (x) are polynomials that describe the seasonal part of the process. The commonly used time series models are represented in this package by objects of the generic form model[param1, param2,...]. Each of these objects serves to specify a particular model and does not itself evaluate to anything. They can be entered as arguments of time series functions as well as generated as output. ARModel[philist,  2] 2] | AR( p) model with p AR coefficients in philist and normally distributed noise with variance  2 2 | MAModel[thetalist,  2] 2] | MA( q) model with q MA coefficients in thetalist and normally distributed noise with variance  2 2 | ARMAModel[philist, thetalist,  2] 2] | ARMA( p, q) model with p AR and q MA coefficients in philist and thetalist, respectively, and normally distributed noise with variance  2 2 | ARIMAModel[d, philist, thetalist,  2] 2] | ARIMA( p, d, q) model with p AR and q MA coefficients in philist and thetalist, respectively, and normally distributed noise with variance  2 2 | SARIMAModel[{d, D}, s, philist, Philist, thetalist, Thetalist,  2] 2] | SARIMA( p, d, q)(P, D, Q) s model with p regular and P seasonal AR coefficients in philist and Philist and q regular and Q seasonal MA coefficients in thetalist and Thetalist, respectively, and normally distributed noise with variance  2 2 |
Time series models. Here, when model is used as a Mathematica function argument it means the model object defined above. The notation philist denotes a list of AR coefficients { 1, 1,  2, ... , 2, ... ,  p} p}, thetalist specifies a list of MA coefficients { 1, 1,  2, ... , 2, ... ,  q} q}, and so on. The noise is zero-mean Gaussian white noise, and its variance or covariance matrix will be called the noise parameter. d (or D) is the order of differencing, and s is the seasonal period. To extract any of these arguments from a model, we can use the function Part or one of the following functions. | ARCoefficients[model] | extract the AR coefficients of model | | MACoefficients[model] | extract the MA coefficients of model | | SeasonalARCoefficients[model] | extract the seasonal AR coefficients of model | | SeasonalMACoefficients[model] | extract the seasonal MA coefficients of model | | SeasonalPeriod[model] | extract the seasonal period of model | | DifferencingOrder[model] | extract the differencing order of model | | NoiseParameter[model] | extract the noise parameter of model |
Functions extracting the parameters of time series models. All of the functions in this package with the exception of AsymptoticCovariance and the functions analyzing ARCH models work for both univariate and multivariate cases, although some are illustrated using examples of univariate series only. ARMAModel[{0.5, -0.2}, {0.7}, 0.8] represents the ARMA( 2, 1) model Xt-0.5Xt-1+0.2Xt-2=Zt+0.7Zt-1 with noise variance 0.8. Note that it does not evaluate to anything. | Out[2]= | 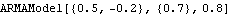 |
We can extract the MA coefficient using MACoefficients. | Out[3]= | 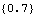 |
We can also use the function Part to extract the argument. | Out[4]= | 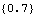 |
This is a SARIMA( 2, 2, 1)( 1, 3, 0) 4 model. Note that the absence of the seasonal MA part is represented by "thetalist"={ } (or "thetalist"={0}). | Out[5]= | 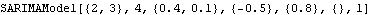 |
This is how we get the differencing orders of both the seasonal and ordinary parts. | Out[6]= | 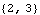 |
| ToARModel[model, n] | give the AR( n) model that is the order n truncation of the AR( 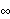 ) expansion of model | | ToMAModel[model, n] | give the MA( n) model that is the order n truncation of the MA( 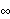 ) expansion of model | | ToARMAModel[model] | convert an ARIMA or a SARIMA model to an ARMA model |
Conversions of time series models. This computes the first four coefficients in the expansion of an AR(1) model as an MA( 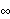 ) model and returns the corresponding MA(4) model. | Out[7]= | 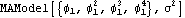 |
The first four coefficients in the expansion of an ARMA( 1, 1) model as an AR( 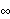 ) model are calculated and the corresponding AR(4) model is returned. | Out[8]= | 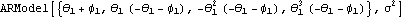 |
This computes the first three coefficients in the expansion of a vector AR(2) model as an MA( 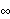 ) model and returns the corresponding vector MA(3) model. | Out[9]= | 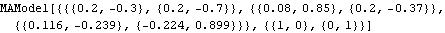 |
This converts an ARIMA( 2, 2, 1) into the equivalent ARMA( 4, 1) model. | Out[10]= | 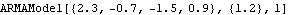 |
This converts a SARIMA (1, 2, 1)(1, 1, 1)2 model into the equivalent ARMA( 7, 3) model. | Out[11]= |  |
Given a model, its covariance function and correlation function can be calculated. For a univariate zero-mean, stationary process, the covariance function at lag h is defined by  (h)=E(Xt+hXt) (h)=E(Xt+hXt) ( E denotes the expectation); the correlation function, by 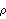 (h)= (h)= (h)/ (h)/ (0) (0). For a multivariate process, the matrix covariance function is defined by 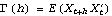 ( X denotes the transpose of X), and the matrix correlation function at lag h, R(h), is given by 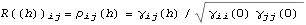 where  ij(h)= ij(h)=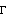 ((h))ij ((h))ij. Another useful function is the partial correlation function. The partial correlation function at lag k,  k, k k, k, is defined to be the correlation between Xt+k and Xt with all intervening variables fixed. The power spectrum of a univariate ARMA( p, q) process is given by 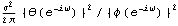 , and for a multivariate process the power spectrum is 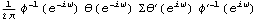 . | StationaryQ[model] | give True if model is stationary, False otherwise | | StationaryQ[philist] | give True if the model with its AR coefficients in philist is stationary, False otherwise | | InvertibleQ[model] | give True if model is invertible, False otherwise | | InvertibleQ[thetalist] | give True if the model with its MA coefficients in thetalist is invertible, False otherwise | | CovarianceFunction[model, n] | give the covariance function of model up to lag n | | CorrelationFunction[model, n] | give the correlation function of model up to lag n | | PartialCorrelationFunction[model, n] | give the partial correlation function of model up to lag n | Spectrum[model,  ] ] | give the power spectrum of model as a function of  |
Properties of time series models. This time series model has the AR polynomial  (x)=1-0.5x+0.2x2-1.5x3 (x)=1-0.5x+0.2x2-1.5x3.  (x)=0 (x)=0 has roots inside the unit circle, so the process is not stationary. | Out[12]= | 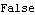 |
We can also just enter the AR coefficients to check stationarity. | Out[13]= | 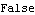 |
These vector AR coefficients indicate a stationary process. The noise covariance can be omitted as we have done here since it is irrelevant for determining stationarity. | Out[14]= | 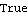 |
A given time series model has the MA polynomial  (x)=1+0.3x-0.1x2 (x)=1+0.3x-0.1x2. The roots of  (x)=0 (x)=0 are all outside the unit circle, so the process is invertible. | Out[15]= | 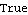 |
This gives the covariance function  (h) (h) of an MA(1) model for h=0, 1, 2, 3. Note that for an MA( q) model  (h)=0 (h)=0 for h>q. | Out[16]= | 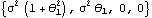 |
This yields the covariance function of a vector ARMA(1, 1) model up to lag 2. | Out[17]= | 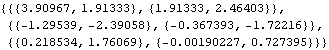 |
The correlation function of an AR(1) model is calculated up to lag 5. | Out[18]= | 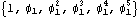 |
This gives the partial correlation function  k, k k, k of an AR(2) model at lags k=1, 2, 3, and 4. Note that the partial correlation function starts at lag 1, and for an AR(p) process,  k, k=0 k, k=0 for k>p. | Out[19]= | 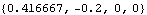 |
Here is the power spectrum of an ARMA(1, 1) model as a function of  . | Out[20]= | 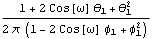 |
This yields the plot of the spectrum calculated above with  1=0.7 1=0.7 and  1=-0.2 1=-0.2. | Out[21]= | 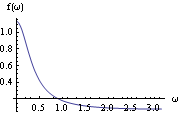 |
RandomSequence[ , ,  2, n] 2, n] | generate a random sequence of length n distributed normally with mean  and variance  2 2 | | TimeSeries[model, n] | generate a time series of length n from model | | TimeSeries[model, n, {x-p+1, x-p+2, ..., x0} ] | generate a time series with p given initial values | | TimeSeries[model, n, {z-q+1, z-q+2, ..., zn}, {x-p+1, x-p+2, ..., x0} ] | generate a time series with a given noise sequence {z} and initial values {x} |
Generating random sequences and time series. Both RandomSequence and TimeSeries uses the current default random number generator. Sequences generated prior to Version 6.0 of Mathematica can be obtained by including the option LegacySequence→True. A sequence of 5 random numbers is generated. They are normally distributed with mean 0 and variance 1.2. | Out[22]= | 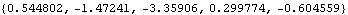 |
This generates a sequence of 4 random vectors distributed normally with mean {0.5, 0.7 } and covariance matrix {{0.9, -0.2}, {-0.2, 1.0}}. Note that we have used SeedRandom[1039] to start the random number generator with seed 1039. | Out[23]= | 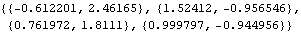 |
Here is a scalar time series of length 7 generated from the ARMA(2, 1) model Xt-0.5Xt-1+0.2Xt-2=Zt+0.7Zt-1. The normally distributed noise has a mean 0 and a variance of 0.8. | Out[24]= | 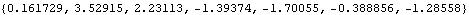 |
This generates a time series {x1, x2, ... , x7} from the same model as above with given values of x-1=-0.3, and x0=0.5. | Out[25]= | 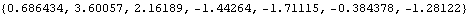 |
Here is a vector time series of length 5 generated from a vector MA(2) model. Note that the MA parameters and the noise covariance are now matrices. | Out[26]= | 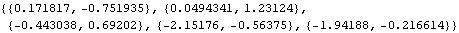 |
This generates a scalar time series of length 8 from the SARIMA(2, 2, 2)(2, 1, 1) 2 model (1-B)2 (1-B2) (0.2 B2-0.5 B+1) (0.1 B4-0.3 B2+1) Xt =(1+0.6B-0.1B2)(1-0.5B2)Zt with noise variance 0.9. | Out[27]= | 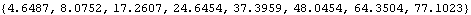 |
|