|
2.4 Univariate ARCH and GARCH ModelsAutoregressive Conditional Heteroskedasticity (ARCH) models and Generalized Autoregressive Conditional Heteroskedasticity (GARCH) models are used to model the changes in variance as a function of time. A GARCH( p, q) model is where {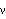 t} t} is an independently distributed Gaussian random sequence with zero mean and unit variance; ht is the conditional variance of Zt conditional on all the information up to time t-1, It-1: When p=0, we have an ARCH( q) model. A GARCH-in-mean (or ARCH-in-mean) model is defined by That is, the conditional mean is also a function of conditional variance ht, where f(h) is usually 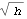 or h. An ARCH (or GARCH) regression model is | ARCHModel[alphalist] | ARCH( q) model with the coefficients {  0 0,  1 1,...,  q q} in alphalist | | GARCHModel[alphalist, betalist] | GARCH( p, q) model with the coefficients {  0 0,  1 1,...,  q q} and { 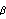 1 1,..., 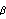 q q} in alphalist and betalist, respectively | ARCHModel[alphalist, 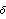 , f] , f] | ARCH-in-mean model | GARCHModel[alphalist, betalist, 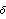 , f] , f] | GARCH-in-mean model |
ARCH and GARCH models. Note that the function f should be a symbol representing a Mathematica built-in function or a pure function. Note also these models will be referred as archmodel to differentiate them from ARMA type models. | TimeSeries[archmodel, n] | generate a time series of length n from archmodel | | TimeSeries[archmodel, n, init] | generate a time series with given initial values init |
Generating ARCH time series. This generates a GARCH time series of length 10. Note that the third argument is optional. It specifies the initial values {{h-p+1, h-p+2, ..., h0}, {z-q+1, z-q+2, ..., z0}}, or {z-q+1, z-q+2, ..., z0} as in the case of an ARCH model. | Out[2]= | 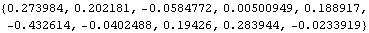 |
Here we generate an ARCH-in-mean series of length 10. Note that the function f should be a symbol representing a Mathematica built-in function (here Log) or a pure function. | Out[3]= | 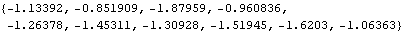 |
This generates the so-called AR-ARCH series. That is, the noise or error used in generating AR series is an ARCH process, with  0=0.02 0=0.02 and  1=0.3 1=0.3. | Out[4]= | 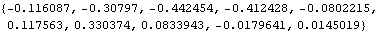 |
| LogLikelihood[data, archmodel] | give the logarithm of the Gaussian likelihood for the given data and archmodel | | LogLikelihood[data, archmodel, X, blist] | give the logarithm of the Gaussian likelihood of an ARCH or GARCH regression series data | | LogLikelihood[data, archmodel, ARModel[philist]] | give the logarithm of the Gaussian likelihood of an AR-ARCH or AR-GARCH series data | LogLikelihood[data, archmodel, ARModel[philist], 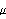 ] ] | give the logarithm of the Gaussian likelihood of an AR-ARCH or AR-GARCH series with a constant mean 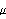 |
Log likelihood for ARCH series. | option name | default value | | | "PresampleValue" | Automatic | presample value |
Option for LogLikelihood. Note that the X is the matrix 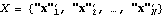 and blist is a list of parameters "b" defined in the ARCH regression model. The presample values of 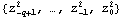 and {h-p+1, ..., h-1, h0} are assumed to be equal to a fixed value sigma2, and it can be specified using the option PresampleValue -> sigma2. The default setting for PresampleValue is Automatic, which corresponds to using the sample equivalence of 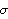 2 2 for GARCH models and to using  0/(1- 0/(1-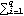  i- i-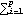 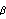 i) i) for GARCH-in-mean models. This gives the log likelihood of data. | Out[5]= | 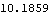 |
| ConditionalMLEstimate[data, archmodel] | fit archmodel to data using the conditional maximum likelihood method | | ConditionalMLEstimate[data, archmodel, X, blist] | fit ARCH or GARCH regression model to data | | ConditionalMLEstimate[data, archmodel, ARModel[philist]] | fit AR-ARCH or AR-GARCH model to data | ConditionalMLEstimate[data, archmodel, ARModel[philist], 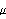 ] ] | fit nonzero mean AR-ARCH or AR-GARCH model to data |
Conditional maximum likelihood estimations. | option name | default value | | | MaxIterations | 30 | maximum number of iterations in searching for minimum | | PresampleValue | Automatic | presample value |
Options for ConditionalMLEstimate. This generates a GARCH-in-mean series of length 200. ConditionalMLEstimate is used to estimate the model parameters. Note that the output contains the estimated model and the root mean square errors of the estimated parameters. | Out[7]= | 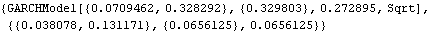 |
We generate an AR-ARCH series of length 50. This gives the conditional maximum likelihood estimate of the model parameters and their corresponding root mean square errors. | Out[9]= | 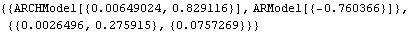 |
Note that we can also first estimate the parameter of the AR model. | Out[10]= | 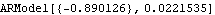 |
Then we estimate the ARCH parameters from the residuals. The two estimates give comparable results. | Out[11]= | 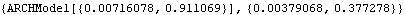 |
| LMStatistic[data, archmodel] | calculate LM statistic with estimated parameters under the null inside archmodel | | LMStatistic[data, archmodel, X, blist] | calculate LM statistic of an ARCH or GARCH regression series | | LMStatistic[data, archmodel, ARModel[philist]] | calculate LM statistic of an AR-ARCH or AR-GARCH series | LMStatistic[data, archmodel, ARModel[philist], 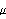 ] ] | calculate LM statistic of an AR-ARCH or AR-GARCH series with nonzero mean  |
LM statistic. | option name | default value | | | PresampleValue | Automatic | presample value |
Option for LMStatistic. To test the existence of ARCH using the LM test, we need to estimate the parameters under the null hypothesis. Note that the null hypothesis is no ARCH, that is, a pure AR(1) model. | Out[12]= | 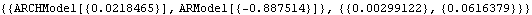 |
This is the alternative model with the parameters estimated under the null hypothesis. Note that  1=0 1=0 is inserted. | Out[13]= | 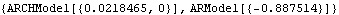 |
This gives the LM statistic. | Out[14]= | 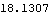 |
Since this number is larger than the the above LM statistic, the null hypothesis is accepted. | Out[15]= | 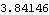 |
|