1.7.2 Large Sample Approximation to the Best Linear Predictor It turns out that in the large sample limit ( n→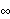 ) the best linear predictor can be derived and calculated in a much simpler fashion. In the following we derive the best linear predictor in the infinite sample case, and from there derive an approximate formula for calculating the best linear predictor when n is large. Best Linear Predictor in the Infinite Sample CaseA stationary ARMA( p, q) process at time n+h is given by Since Xt is a random variable, it is reasonable to use its expectation as our predicted value, taking into account the information we have for Xt at t=n, n-1, ... . (This subsection is the only place where we assume that we have data extending to the infinite past.) So if 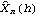 denotes the forecast h steps ahead, we define 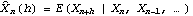 , the conditional expectation of Xn+h given {Xn, Xn-1, ... }. On taking the conditional expectation on both sides of ( 7.1) and letting 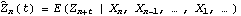 , we obtain, Equation ( 7.2) can be used recursively to obtain the forecast values of Xn+h for h=1, 2, ... once we know the right-hand side of ( 7.2). It is easy to see that for h≤0, 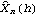 and 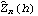 are simply the realized values of Xn+h and Zn+h, respectively, and for h>0, since the future values of the noise are independent of Xt ( t≤n), we have 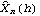 obtained from ( 7.2) using ( 7.3) to ( 7.5) is, in fact, the best linear predictor. To see this we show that the mean square forecast error of 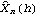 is minimum. Consider an arbitrary predictor 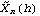 which is linear in Xi, i≤n. It can be rewritten in terms of {Zt} as 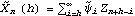 . The sum starts at i=h because future noise has no influence on our prediction. Now consider its mean square error where we have used the expansion Xn+h=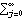  jZn+h-j jZn+h-j (see ( 2.9)). The mean square error in ( 7.6) achieves its minimum value if 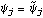 . But this is exactly the case for the expansion of 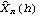 in terms of {Zt} since ( 7.2) has the same form as the ARMA equation governing Xn+h, ( 7.1). Therefore, 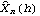 is the desired best linear predictor. Its forecast error is given by and its mean square forecast error is given by Approximate Best Linear PredictorWhere does the assumption of an infinite sample enter in the above derivation? It is used when we replace E(Zt Xn, Xn-1, ... ) Xn, Xn-1, ... ) by Zt for t≤n (see ( 7.4)). This is true only if we know the series all the way back to the infinite past ( i.e., we have an infinite sample) since knowing a finite number of data points Xn, ... , X1 does not determine Zt completely. To see this we recall that an invertible ARMA model can be written as Zt= -1(B) -1(B) (B)Xt= (B)Xt=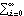  iXt-i iXt-i. So only if we have infinite data points can we replace the conditional expectation by Zt. Although in practice we invariably have a finite number of observations, the above derivation of the best linear predictor in the infinite sample limit nevertheless enables us to develop a way of calculating the approximate best linear predictor when n is large. Let 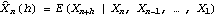 and 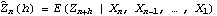 . For an invertible model, the  weights decrease exponentially, and for large n it is a good approximation to truncate the infinite sum and write, Note that Zn+h in ( 7.9) is just the residual defined in ( 6.6) since truncating the infinite sum is the same as setting Xt=0 for t≤0. Under this approximation we again arrive at 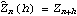 for h≤0, the same result as in ( 7.4). With ( 7.3) to ( 7.5) and ( 7.9), ( 7.2) provides a recursive way of computing the predicted values of Xn+h for h=1, 2, ... . This is often used as an approximate best linear predictor in the finite but large sample case to speed up the calculation. However, we must keep in mind that only when n is sufficiently large and the model is invertible is the approximation good. Although ( 7.9) is used to get the approximate predictor for the finite sample case, the mean square error of the best linear predictor in the infinite sample case, ( 7.8), is used to approximate that in the finite sample case. This can underestimate the real error corresponding to the given predictor, but it makes little difference when the model is invertible and n is large. To get the approximate best linear predictor and its mean square error defined by ( 7.2) to ( 7.5), ( 7.9), and ( 7.8), we can simply use the same function for getting the exact best linear predictor BestLinearPredictor and set its option Exact to False. In the rest of the section we give some examples of using BestLinearPredictor to get both exact and approximate best linear predictions. Example 7.2 For an AR(1) process Xt+1= 1Xt+Zt 1Xt+Zt, ( 7.2) gives 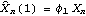 and 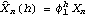 . The mean square error is 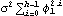 , which is obtained by first noting that 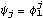 and by using ( 7.8). These are the predicted values and their mean square errors. | Out[6]= | 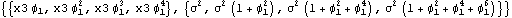 |
We see that for a stationary time series the predicted value converges to the mean of the series (=0) and the mean square error of the forecast converges to the variance of the series (=  2 2) for large h. Also when the time series is an AR process, Zn+h for h≤0 does not appear in ( 7.2), so the assumption of infinite sample does not come in and no approximation is made. So even if we set Exact -> False, ( 7.2) to ( 7.5) and ( 7.8) give the exact finite sample best linear predictor and its mean square error. However, when the MA part is present, the approximation can make a difference as in the following example. Example 7.3 Given the first 15 data points of a time series generated from the MA(2) process Xt=Zt+0.5Zt-1-1.2Zt-2 (  2=1 2=1), find the predictions for the next four data points and their mean square errors. We first define the model as ma2 to avoid repeated typing. The random number generator is seeded first. This generates a time series of length 15. These are the exact best linear predictions and their mean square errors. | Out[10]= | 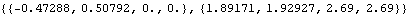 |
However, if we try to perform the same calculation approximately, we obtain different results. This gives the approximate best linear predictions. | Out[11]= | 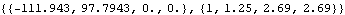 |
The reason that we get totally different forecasts is that the model is not invertible. The model is not invertible. | Out[12]= | 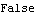 |
So the approximation ( 7.9) is not valid. On the other hand, for an invertible model and a large data set, the approximation can be very good and it is often used to speed up calculations. The following example is for an invertible MA(2) model with 100 data points. Example 7.4 Calculate the prediction for the next four data points given the first 100 data points generated from the model Xt=Zt-0.5Zt-1+0.9Zt-2. The noise variance is 1. We define the model to be model. The random number generator is seeded first. This generates the time series. The exact best linear prediction is obtained. | Out[16]= | 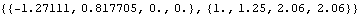 |
This yields the approximate best linear prediction. | Out[17]= | 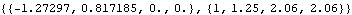 |
Again 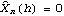 for h>q. (See the remark after Example 7.1.) Also for an MA model  j= j= j j (  0 0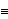 1 1) the mean square error given by ( 7.8) is 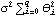 for h>q. A natural question is how large n has to be in order to get a very good approximation to the best linear prediction. It depends on how close to the unit circle the zeros of the MA polynomial are. The closer the zeros are to the unit circle, the slower the  weights decrease and the larger the n required to ensure the validity of ( 7.9). We can explicitly find the absolute values of the roots of  (x)=0 (x)=0 in the above example. Here are the absolute values of the roots. | Out[18]= | 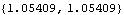 |
It appears that n=100 gives an adequate approximation. Example 7.5 For the invertible ARMA(1, 2) process Xt-0.9Xt-1=Zt-0.4Zt-1+0.8Zt-2, the two roots of  (x)=0 (x)=0 have an absolute value around 1.12. We expect that the approximation will be good even for moderate n. This is indeed the case as we see below. The random number generator is seeded. This generates a time series of length 50. This yields the exact best linear prediction. | Out[22]= | 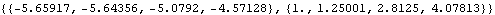 |
Here is the approximate best linear prediction. | Out[23]= | 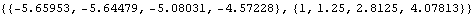 |
We see that in this case for n=50 the approximate prediction is in good agreement with the exact best linear prediction. |