When the ARMA model
 (B)Xt=
(B)Xt= (B)Zt
(B)Zt is not stationary, the equation
 (x)=0
(x)=0 (or
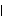
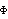 (x)
(x)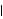 =0
=0 in the multivariate case) will have at least one root inside or on the unit circle. In this case, the methods of analyzing stationary time series cannot be used directly. However, the stationary ARMA models introduced in Section
1.2 can be generalized to incorporate a special class of nonstationary time series models. This class of models is characterized by all the zeros of the AR polynomial being outside the unit circle with the exception of
d of them which are 1. In other words, this class of nonstationary models is defined by
where
d is a non-negative integer,
 (x)
(x) and
 (x)
(x) are polynomials of degrees
p and
q, respectively, and all the roots of
 (x)=0
(x)=0 are outside the unit circle. Equation (
3.1) defines an autoregressive integrated moving average process of orders
p,
d,
q, or simply, ARIMA(
p,
d,
q).
Using the definition of the backward shift operator
B, we have
(1-B)Xt=Xt-Xt-1. This operation is for obvious reasons called
differencing the time series. (We use
(1-B)2Xt=(1-B)(Xt-Xt-1)=Xt-2Xt-1+Xt-2 to difference the time series twice.) Equation (
3.1) says that if
{Xt} is nonstationary and satisfies (
3.1), then after differencing the time series
d times the differenced series
{Yt} (
Yt=(1-B)dXt) is stationary and satisfies
 (B)Yt=
(B)Yt= (B)Zt
(B)Zt, that is, an ARMA(
p,
q) process. Note that we can view
{Yt} as a filtered version of
{Xt} (see Section
1.4.3).
Therefore, any ARIMA(
p,
d,
q) series can be transformed into an ARMA(
p,
q) series by differencing it
d times and, thus, the analysis of an ARIMA process does not pose any special difficulty as long as we know the number of times to difference (
i.e.,
d) the series. We will see in Section
1.4.3 how the differencing is done in practice.
An ARIMA(
p, 0,
q) process is simply an ARMA(
p,
q) process.