In the time domain we have investigated the covariance or correlation function of a stationary time series. Alternatively, we can study the
(power) spectral density function or simply the
(power) spectrum as a function of the frequency

. The spectrum of a stationary time series
f( )
) is the counterpart of a covariance function in frequency domain. That is, it is the Fourier transform of the covariance function
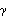 (k)
(k) and vice versa:
Here the covariance function
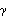 (k)
(k) is assumed to satisfy
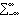
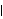
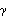 (k)
(k)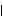 <
<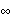
(
i.e.,
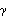 (k)
(k) is
absolutely summable). Since
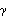 (k)=
(k)=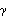 (-k)
(-k), (
8.1) can also be written as
We can immediately identify the following properties of the spectrum
f( )
): (a)
f( )
) is
2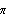
-periodic, that is,
f( )=f(
)=f( +2
+2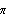 j)
j) (
j integer), and (b)
f( )
) is real and even (
f( )=f(-
)=f(- )
)). These properties of
f( )
) make it sufficient to consider the spectrum in the range
0≤ ≤
≤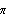
.
Setting
k=0 in (
8.2), we have
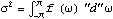
. We see that the total variance of the process can be "decomposed" into contributions from different frequencies, and
f( )"d"
)"d"
represents the contribution to the total variance of the components in the frequency range (
 ,
,  +"d"
+"d"
).
Again we caution the reader that conventions differ. Some authors define the spectrum with different factors. Others use the correlation function instead of covariance function in (
8.1) to define the spectrum. We call this the normalized spectrum and use (
8.1) as our definition of the spectrum.
The covariance function of a white noise process is given by
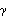 (0)=
(0)=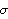 2
2,
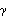 (k)=0
(k)=0 for
k≠0. From (
8.1) its spectrum is
f( )=
)=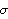 2/(2
2/(2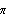 )
). It is independent of

and its plot against frequency is "flat". This means that each frequency contributes equally to the variance and thus the name white noise.