Legacy Documentation

The fundamental assumption of time series modeling is that the value of the series at time t, X_t, depends only on its previous values (deterministic part) and on a random disturbance (stochastic part). Furthermore, if this dependence of X_t on the previous p values is assumed to be linear, we can write

where {₁, ₂, ... , _p} are real constants. 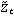is the disturbance at time t, and it is usually modeled as a linear combination of zero-mean, uncorrelated random variables or a zero-mean white noise process {Z_t}

({Z_t} is a white noise process with mean 0 and variance ² if and only if EZ_t=0, 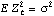for all t, and EZ_sZ_t=0 if s≠t, where E denotes the expectation.) Z_t is often referred to as the random error or noise at time t. The constants {₁, ₂, ... , _p} and {₁, ₂, ... , _q} are called autoregressive (AR) coefficients and moving average (MA) coefficients, respectively, for the obvious reason that (2.1) resembles a regression model and (2.2) a moving average. Combining (2.1) and (2.2) we get

This defines a zero-mean autoregressive moving average (ARMA) process of orders p and q, or ARMA(p, q). In general, a constant term can occur on the right-hand side of (2.3) signalling a nonzero mean process. However, any stationary ARMA process with a nonzero mean can be transformed into one with mean zero simply by subtracting the mean from the process. (See Section 1.2.2 for the definition of stationarity and an illustrative example.) Therefore, without any loss of generality we restrict our attention to zero-mean ARMA processes.

It is useful to introduce the backward shift operator B defined by

This allows us to express compactly the model described by (2.3). We define the autoregressive polynomial (x) as

and the moving average polynomial (x) as

and assume that (x) and (x) have no common factors. (Note the negative signs in the definition of the AR polynomial.) Equation (2.3) can be cast in the form

When q=0 only the AR part remains and (2.3) reduces to a pure autoregressive process of order p denoted by AR(p)

Similarly, if p=0, we obtain a pure moving average process of order q, MA(q),

When neither p nor q is zero, an ARMA(p, q) model is sometimes referred to as a "mixed model".

The commonly used time series models are represented in this package by objects of the generic form model["\!\(\*StyleBox[\"\\\"param\\\"\", \"TI\"]\)"₁, "\!\(\*StyleBox[\"\\\"param\\\"\", \"TI\"]\)"₂, ... ]. Since an ARMA model is defined by its AR and MA coefficients and the white noise variance (the noise is assumed to be normally distributed), the object

ARMAModel[{₁, ₂, ... , _p}, {₁, ₂, ... , _q},²]

specifies an ARMA(p, q) model with AR coefficients {₁, ₂, ... , _p} and MA coefficients {₁, ₂, ... , _q} and noise variance ². Note that the AR and MA coefficients are enclosed in lists. Similarly, the object

ARModel[{₁, ₂, ... , _p},²]

specifies an AR(p) model and

MAModel[{₁, ₂,... , _q},²]

denotes an MA(q) model. Each of these objects provides a convenient way of organizing the parameters and serves to specify a particular model. It cannot itself be evaluated. For example, if we enter an MAModel object it is returned unevaluated.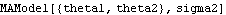

These objects are either used as arguments of time series functions or generated as output, as we will see later in examples.