1.2.2 Stationarity In order to make any kind of statistical inference from a single realization of a random process, stationarity of the process is often assumed. Intuitively, a process {Xt} is stationary if its statistical properties do not change over time. More precisely, the probability distributions of the process are time-invariant. In practice, a much weaker definition of stationarity called second-order stationarity or weak stationarity is employed. Let E denote the expectation of a random process. The mean, variance, and covariance of the process are defined as follows: mean:  (t)=EXt (t)=EXt, variance:  2(t)="Var"(Xt)=E(Xt- 2(t)="Var"(Xt)=E(Xt- (t))2 (t))2, and covariance:  (s, r)="Cov"(Xs, Xr)=E(Xs- (s, r)="Cov"(Xs, Xr)=E(Xs- (s))(Xr- (s))(Xr- (r)) (r)). A time series is second-order stationary if it satisfies the following conditions:
(a)  (t)= (t)= , and  2(t)= 2(t)= 2 2 for all t, and (b)  (s, r) (s, r) is a function of (s-r) only. Henceforth, we will drop the qualifier "second-order" and a stationary process will always refer to a second-order or weak stationary process.
By definition, stationarity implies that the process has a constant mean  . This allows us without loss of generality to consider only zero-mean processes since a constant mean can be transformed away by subtracting the mean value from the process as illustrated in the following example. Example 2.1 Transform a nonzero mean stationary ARMA( p, q) process to a zero-mean one. A nonzero mean stationary ARMA( p, q) model is defined by  (B)Xt= (B)Xt=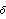 + + (B)Zt (B)Zt, where 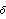 is a constant and  (x) (x) and  (x) (x) are AR and MA polynomials defined earlier. Taking the expectation on both sides we have  (1) (1) = =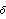 or  = =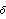 / / (1) (1). (For a stationary model we have  (1)≠0 (1)≠0. See Example 2.2.) Now if we denote Xt- as Yt, the process {Yt} is a zero-mean, stationary process satisfying  (B)Yt= (B)Yt= (B)Zt (B)Zt. There is another important consequence of stationarity. The fact that the covariance "Cov"(Xs, Xr) of a stationary process is only a function of the time difference s-r (which is termed lag) allows us to define two fundamental quantities of time series analysis: covariance function and correlation function. The covariance function  (k) (k) is defined by and the correlation function 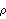 (k) (k) is Consequently, a correlation function is simply a normalized version of the covariance function. It is worth noting the following properties of 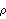 (k) (k): 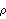 (k)= (k)=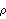 (-k) (-k), 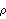 (0)=1 (0)=1, and 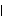 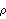 (k) (k)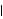 ≤1 ≤1. Before we discuss the calculation of these functions in the next section, we first turn to the ARMA models defined earlier and see what restrictions stationarity imposes on the model parameters. This can be seen from the following simple example. Example 2.2 Derive the covariance and correlation functions of an AR(1) process Xt= 1Xt-1+Zt 1Xt-1+Zt. From ( 2.8) we obtain the covariance function at lag zero 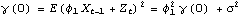 , and hence, 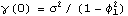 . Now  (k)=E(Xt+kXt)=E(( (k)=E(Xt+kXt)=E(( 1Xt+k-1+Zt+k)Xt)= 1Xt+k-1+Zt+k)Xt)= 1 1 (k-1) (k-1). Iterating this we get 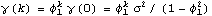 and the correlation function 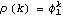 . (Note that we have used EXtZt+k=0 for k>0.) In the above calculation we have assumed stationarity. This is true only if 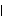  1 1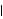 <1 <1 or, equivalently, the magnitude of the zero of the AR polynomial  (x)=1- (x)=1- 1x 1x is greater than one so that  (0) (0) is positive. This condition of stationarity is, in fact, general. An ARMA model is stationary if and only if all the zeros of the AR polynomial  (x) (x) lie outside the unit circle in the complex plane. In contrast, some authors refer to this condition as the causality condition: an ARMA model is causal if all the zeros of its AR polynomial lie outside the unit circle. They define a model to be stationary if its AR polynomial has no zero on the unit circle. See for example, Brockwell and Davis (1987), Chapter 3. A stationary ARMA model can be expanded formally as an MA( 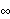 ) model by inverting the AR polynomial and expanding  -1(B) -1(B). From ( 2.6), we have where { j} j} are the coefficients of the equivalent MA( 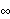 ) model and are often referred to as  weights. For example, an AR(1) model can be written as 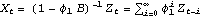 , i.e., 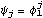 . Similarly, we say an ARMA model is invertible if all the zeros of its MA polynomial lie outside the unit circle, and an invertible ARMA model in turn can be expanded as an AR(  ) model Note the symmetry or duality between the AR and MA parts of an ARMA process. We will encounter this duality again later when we discuss the correlation function and the partial correlation function in the next two sections. To check if a particular model is stationary or invertible, the following functions can be used: StationaryQ[model] or StationaryQ[{ 1, 1, ... ,  p}] p}] InvertibleQ[model] or InvertibleQ[{ 1, 1, ... ,  q}] q}]. (Henceforth, when model is used as a Mathematica function argument it means the model object.) When the model coefficients are numerical, these functions solve the equations  (x)=0 (x)=0 and  (x)=0 (x)=0, respectively, check whether any root has an absolute value less than or equal to one, and give True or False as the output. Example 2.3 Check to see if the ARMA(2, 1) model Xt-0.5Xt-1+1.2Xt-2=Zt+0.7Zt-1 is stationary and invertible. (The noise variance is 1.) The model is not stationary. | Out[3]= | 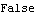 |
Since the stationarity condition depends only on the AR coefficients, we can also simply input the list of AR coefficients. This gives the same result as above. | Out[4]= | 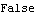 |
We can, of course, use Mathematica to explicitly solve the equation  (x)=0 (x)=0 and check that there are indeed roots inside the unit circle. This solves the equation  (x)=0 (x)=0. | Out[5]= | 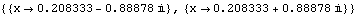 |
This gives the absolute values of the two roots. In Mathematica, % represents the last output and Abs[x /. %] substitutes the roots in x and finds the absolute values. | Out[6]= | 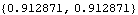 |
We can check invertibility using the function InvertibleQ. The model is found to be invertible. | Out[7]= | 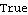 |
We can also just input the MA coefficients to check invertibility. | Out[8]= | 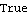 |
Thus the model under consideration is invertible but not stationary. The functions StationaryQ and InvertibleQ give True or False only when the corresponding AR or MA parameters are numerical. The presence of symbolic parameters prevents the determination of the locations of the zeros of the corresponding polynomials and, therefore, stationarity or invertibility cannot be determined, as in the following example. No True or False is returned when the coefficients of the polynomial are not numerical. | Out[9]= | 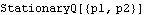 |
Next we define the functions that allow us to expand a stationary ARMA model as an approximate MA( q) model ( Xt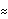 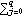  jZt-j jZt-j) using ( 2.9) or an invertible ARMA model as an approximate AR( p) model ( 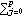  jXt-j jXt-j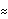 Zt Zt) using ( 2.10). The function gives the order p truncation of the AR( 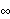 ) expansion of model. Similarly, yields the order q truncation of the MA( 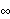 ) expansion of model. The usage of these functions is illustrated in the following example. Example 2.4 Expand the model Xt-0.9Xt-1+0.3Xt-2=Zt as an approximate MA(5) model using ( 2.9) and the model Xt-0.7Xt-1=Zt-0.5Zt-1 as an approximate AR(6) model using ( 2.10). The noise variance is 1. This expands the given AR(2) model as an MA(5) model. | Out[10]= | 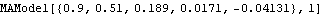 |
In the above calculation, as in some others, the value of the noise variance  2 2 is not used. In this case we can omit the noise variance from the model objects. Here we suppress the noise variance. This does not affect the expansion coefficients. | Out[11]= | 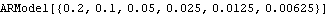 |
We can, of course, include the variance back in the model object using Append. The noise variance is inserted back into the model object. | Out[12]= | 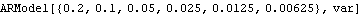 |
If the model is not stationary or invertible, the corresponding expansion is not valid. If we insist on doing the expansion anyway, a warning message will appear along with the formal expansion as seen below. A warning message comes with the expansion result. | Out[13]= | 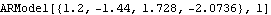 |
These functions can also be used to expand models with symbolic parameters, but bear in mind that it is usually slower to do symbolic calculations than to do numerical ones. This expands an ARMA(1, 1) model with symbolic parameters. | Out[14]= | 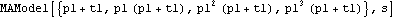 |
|