1.2.4 Partial Correlation FunctionsIn Example 2.1 we calculated the correlation function of an AR(1) process. Although Xt depends only on Xt-1, the correlations at large lags are, nevertheless, nonzero. This should not be surprising because Xt-1 depends on Xt-2, and in turn Xt-2 on Xt-3, and so on, leading to an indirect dependence of Xt on Xt-k. This can also be understood by inverting the AR polynomial and writing Multiplying both sides of the above equation by Xt-k and taking expectations, we see that the right-hand side is not strictly zero no matter how large k is. In other words, Xt and Xt-k are correlated for all k. This is true for all AR( p) and ARMA( p, q) processes with p≠0, and we say that the correlation of an AR or ARMA process has no "sharp cutoff" beyond which it becomes zero. However, consider the conditional expectation E(XtXt-2 Xt-1) Xt-1) of an AR(1) process, that is, given Xt-1, what is the correlation between Xt and Xt-2? It is clearly zero since Xt= 1Xt-1+Zt 1Xt-1+Zt is not influenced by Xt-2 given Xt-1. The partial correlation between Xt and Xt-k is defined as the correlation between the two random variables with all variables in the intervening time {Xt-1, Xt-2, ... , Xt-k+1} assumed to be fixed. Clearly, for an AR( p) process the partial correlation so defined is zero at lags greater than the AR order p. This fact is often used in attempts to identify the order of an AR process. Therefore, we introduce the function PartialCorrelationFunction[model, h], which gives the partial correlation  k, k k, k of the given model for k=1, 2, ... , h. It uses the Levinson-Durbin algorithm, which will be presented briefly in Section 1.6. For details of the algorithm and more about the partial correlation function, see Brockwell and Davis (1987), pp. 162-164. Example 2.10 Let us compute the partial correlation function  k, k k, k of an AR(2) process up to lag 4. Note that in contrast to the correlation function the output of PartialCorrelationFunction starts from lag 1, and  1, 1= 1, 1=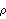 (1) (1). This gives the partial correlation function of an AR(2) model up to lag 4. | Out[30]= | 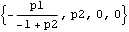 |
We observe that for an AR( p) process  k, k=0 k, k=0 for k>p. Example 2.11 Find the partial correlation function of an MA(1) model. Here the partial correlation function of an MA(1) model up to lag 4 is computed. | Out[31]= | 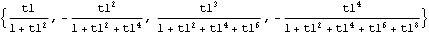 |
The analytic expression for the partial correlation function is  k, k=-(- k, k=-(- )k(1- )k(1- 2)/(1- 2)/(1- 2(k+1)) 2(k+1)), and we see that there is no sharp cutoff in the partial correlation. This property is, in fact, shared by all the MA( q) and ARMA( p, q) models with q≠0. It can be understood by expanding an invertible MA model as an AR(  ) model. Xt is always related to Xt-k with the intervening variables fixed for all k. Observe the duality between the AR and MA models: for an AR( p) model, the partial correlation function  k, k k, k is zero for k>p and the correlation function does not have a sharp cutoff, whereas for an MA( q) model the correlation function  (k) (k) is zero for k>q and the partial correlation function has no sharp cutoff. Here is the plot of the partial correlation function of the MA(1) model in Example 2.11 with  1=0.8 1=0.8. Since the partial correlation function starts from lag 1, in contrast to the correlation function we can use ListLinePlot directly. | Out[32]= | 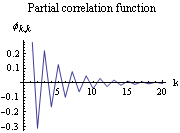 |
|