1.10.3 Testing for ARCHVarious standard procedures are available to test the existence of ARCH or GARCH. A commonly used test is the Lagrange multiplier (LM) test. Consider the null hypothesis that there is no ARCH, that is,  1= 1= 2= 2=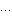 = = q=0 q=0. It is known that (see, for example, Bollerslev (1986), Eqs. (27) and (28)) the LM statistic has an asymptotic 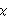 2 2 distribution with q degrees of freedom under the null hypothesis. If the LM statistic evaluated under the null hypothesis is greater than 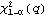 , the null hypothesis is rejected at level  . The function gives the LM statistic, where model is either an ARCH or GARCH model. For an ARCH (or GARCH) regression model ( 10.7), we can use LMStatistic[data, model, X, blist], or if the regression model is an AR model, LMStatistic[data, model, ARModel[philist]], LMStatistic[data, model, ARModel[philist],  ] ], when the AR model has nonzero mean mu. For example, in Example 10.4 we estimated the ARCH-in-mean model with q=1. We can test the hypothesis that both conditional mean and variance are in fact constant by testing the null hypothesis q=0. In the Lagrange multiplier test, the parameters used are those obtained under the null hypothesis. So we first estimate the model parameters with q=0. This gives the estimated model parameters under the null hypothesis. | Out[32]= | 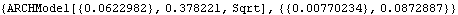 |
The alternative hypothesis is q=1. This is the estimated ARCH-in-mean(1) model obtained under the null hypothesis. | Out[33]= | 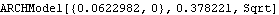 |
Note that under the null hypothesis the series is simply white noise with a mean of 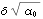 and variance of  0 0. Therefore, we can estimate  0 0 and 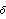 simply using the sample estimates. This gives the sample mean. | Out[34]= | 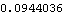 |
This is the sample variance. It is the estimated  0 0. | Out[35]= | 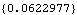 |
This gives the estimated 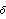 . | Out[36]= | 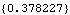 |
The LM statistic is obtained using the model estimated under the null hypothesis. | Out[37]= | 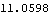 |
The number 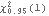 is much smaller than the above lms. So we can reject the null hypothesis of q=0. | Out[38]= | 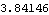 |
Here is another example. Again we first generate an ARCH(3) model. The null hypothesis is an ARCH(1) model and the parameters are estimated under the null hypothesis. | Out[40]= | 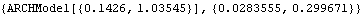 |
The alternative hypothesis is ARCH(3); here we compute the LM statistic for this case. | Out[41]= | 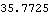 |
The above LM statistic exceeds this number by a large amount. So the null hypothesis of ARCH(1) is rejected. | Out[42]= | 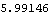 |
Here we generate a GARCH(2,1) series. The null hypothesis is AR(1) and this estimates its parameters. | Out[44]= | 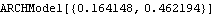 |
In this case there is insufficient evidence to reject the null hypothesis. | Out[45]= | 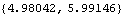 |
Note that it is known that a general test for GARCH( p, q) is not feasible (see Bollerslev (1986)). |