PrimalityProving`
PrimalityProving`
PrimeQCertificate
PrimeQCertificate[n]
gives a certificate that n is prime or that n is composite.
Details and Options
- To use PrimeQCertificate, you first need to load the Primality Proving Package using Needs["PrimalityProving`"].
- PrimeQCertificate uses the Pratt certificate and the Atkin–Morain certificate for primality.
- A certificate of compositeness is a list of three integers, either {a,n-1,n} or {a,2,n}, with
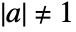 .
. - A prime
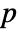 always satisfies
always satisfies 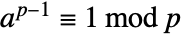 . The certificate {a,n-1,n} can be used to show that n is composite by demonstrating that
. The certificate {a,n-1,n} can be used to show that n is composite by demonstrating that 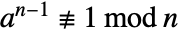 .
. - Any number
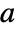 whose square is
whose square is 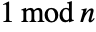 for
for 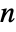 prime must satisfy
prime must satisfy 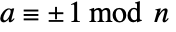 . The certificate {a,2,n} can be used to show that n is composite by demonstrating that
. The certificate {a,2,n} can be used to show that n is composite by demonstrating that 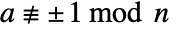 and
and 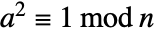 .
. - A certificate of primality consists of a recursive list of certificates which prove that
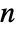 is a prime if one or more smaller numbers are prime as well.
is a prime if one or more smaller numbers are prime as well. - PrimeQCertificate has the same options as ProvablePrimeQ.
Examples
Basic Examples (2)
A certificate that can be used to prove that 1093 is a prime:
The same certificate can be obtained by using ProvablePrimeQ with the option "Certificate"->True:
A certificate that can be used to prove that 1093×3511 is composite:
The output is a list of three integers that indicate 1093×3511 is composite, and that it violates Fermat's little theorem for primes, ![]() if
if ![]() is prime:
is prime: