Curry[f,n]
represents an operator form of the function f of n arguments so that Curry[f,n][x1]…[xn] is equivalent to f[x1,…,xn].
Curry[f]
represents an operator form of the function f of two arguments so that Curry[f][y][x] is equivalent to f[x,y].
Curry[f,{i1,…,in}]
represents an operator form of the function f of n arguments so that Curry[f,{i1,…,in}][x1]…[xn] is equivalent to f[xi1,…,xin].
Curry[f,k{i1,…,in}]
represents a k-arguments operator form of the function f of n arguments so that Curry[f,k{i1,…,in}][x1]…[xk] is equivalent to f[xi1,…,xin], with k≥Max[{i1,…,in}].


Curry
Curry[f,n]
represents an operator form of the function f of n arguments so that Curry[f,n][x1]…[xn] is equivalent to f[x1,…,xn].
Curry[f]
represents an operator form of the function f of two arguments so that Curry[f][y][x] is equivalent to f[x,y].
Curry[f,{i1,…,in}]
represents an operator form of the function f of n arguments so that Curry[f,{i1,…,in}][x1]…[xn] is equivalent to f[xi1,…,xin].
Curry[f,k{i1,…,in}]
represents a k-arguments operator form of the function f of n arguments so that Curry[f,k{i1,…,in}][x1]…[xk] is equivalent to f[xi1,…,xin], with k≥Max[{i1,…,in}].
Details
- Curry[f] is equivalent to Curry[f,{2,1}].
- Curry[f,n] is equivalent to Curry[f,{1,2,…,n}].
- Curry[f,{i1,…,in}] is equivalent to Curry[f,Max[{i1,…,in}]->{i1,…,in}].
- Curry[f,{i1,…,in,opts}][x1]…[xk] is equivalent to f[xi1,…,xin,opts] for a sequence opts of options.
- The ip
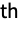 curried argument of Curry[f,{i1,…,in}] will be the p
curried argument of Curry[f,{i1,…,in}] will be the p argument of f.
argument of f. - Curry[f,arity][x1,…][y1,…]…[z1,…] is equivalent to Curry[f,arity][x1,…,y1,…,z1,…], so that the structure of brackets is not relevant, only the number of arguments.
Examples
open all close allBasic Examples (3)
Curry the second argument of a function of two arguments:
Curry a function of three arguments, keeping their order:
This is a curried form of Integrate that curries two integration variables:
Scope (6)
Curry the second argument of a function:
Curry a function of 3 arguments, keeping their order:
Curry a function of 3 arguments, applying a permutation before they are passed to the function:
These are curried operators taking 4 arguments, but only 2 of them are passed to the function f:
Use arguments of the curried operator with any bracketing structure:
Curry Level with default option values:
Pass options to Level:
Applications (5)
Curry Composition of 3 functions:
Feed the 3 functions sequentially:
Apply the composition to an expression:
Specify how many arguments are functions to be composed:
Use Curry to construct the opposite order of a given ordering function:
Build an array of subscripted variables:
Build the K and S combinators using Curry:
The combinations SKK and SKS are equivalent to the identity:
Properties & Relations (6)
Curry[f] is equivalent to Curry[f,{2,1}]:
For a function of zero arguments, Curry[f,0] returns f[]:
If additional arguments are provided, the empty pair of brackets is still inserted:
Compare to Construct:
For positive n, Curry[Construct,n][f] is equivalent to Curry[f,n-1]:
The relation also holds for n=1:
Compose two Curry operators with a permutation and its inverse:
The result is equivalent to using Curry without reordering the arguments:
Take two permutation lists of the same length:
Compose the corresponding Curry operators:
Alternatively, use Curry with their permutation product, in the same order:
See Also
Construct Composition Function Slot Identity Apply Map
Function Repository: ApplyLevel Uncurry FlipFunction
History
Text
Wolfram Research (2018), Curry, Wolfram Language function, https://reference.wolfram.com/language/ref/Curry.html.
CMS
Wolfram Language. 2018. "Curry." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Curry.html.
APA
Wolfram Language. (2018). Curry. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Curry.html
BibTeX
@misc{reference.wolfram_2025_curry, author="Wolfram Research", title="{Curry}", year="2018", howpublished="\url{https://reference.wolfram.com/language/ref/Curry.html}", note=[Accessed: 11-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_curry, organization={Wolfram Research}, title={Curry}, year={2018}, url={https://reference.wolfram.com/language/ref/Curry.html}, note=[Accessed: 11-January-2026]}