PermutationReplace
PermutationReplace[expr,perm]
replaces each part in expr by its image under the permutation perm.
PermutationReplace[expr,gr]
returns the list of images of expr under all elements of the permutation group gr.
Details

- For an integer
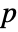 in expr present in the cycles of the permutation perm, the image is the integer to the right of
in expr present in the cycles of the permutation perm, the image is the integer to the right of 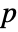 , or the first integer of the cycle if
, or the first integer of the cycle if 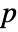 is the last one. For an integer
is the last one. For an integer 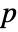 not present in the cycles of perm, the image is
not present in the cycles of perm, the image is 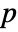 itself.
itself. - If g is a permutation object in expr, then the action is understood as right conjugation: PermutationProduct[InversePermutation[perm],g,perm]. This is equivalent to replacing the points in the cycles of g by their images under perm.
- When applied to a permutation group expr, PermutationReplace operates on each individual generator, returning the same abstract group but acting on different points.
- Both arguments are independently listable. If both arguments are lists then the second argument is threaded first.
Examples
open allclose allBasic Examples (2)
The image of integer 4 under Cycles[{{2,3,4,6}}] is integer 6:
Under the identity, permutation integers are not moved:
An action of a permutation on another permutation is understood as conjugation:
Scope (6)
The image of a point in the support of the permutation is the right neighbor of the point:
The image of the last point of a cycle is the first point of that cycle:
A point not present in the permutation support stays invariant:
PermutationReplace on arrays of integers returns the list of respective images:
PermutationReplace on other permutations is understood as conjugation:
On a permutation group, the generators are conjugated:
The second argument is listable:
If both arguments are lists then the second argument is threaded first:
Properties & Relations (4)
PermutationReplace is a right action with respect to PermutationProduct:
PermutationReplace on an identity permutation list coincides with PermutationList:
PermutationReplace on an identity permutation list produces the inverse result of Permute:
The orbit of a point under a permutation group is the union of the images of that point under the elements of the group:
Text
Wolfram Research (2010), PermutationReplace, Wolfram Language function, https://reference.wolfram.com/language/ref/PermutationReplace.html.
CMS
Wolfram Language. 2010. "PermutationReplace." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PermutationReplace.html.
APA
Wolfram Language. (2010). PermutationReplace. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PermutationReplace.html