RandomPolyhedronCopy to clipboard.
✖
RandomPolyhedron
Copy to clipboard.
✖
RandomPolyhedron[spec]
gives a pseudorandom polyhedron with the specified specification spec.
Details and Options
- RandomPolyhedron gives a Polyhedron drawn from a specific distribution.
- RandomPolyhedron is typically used in testing and verification of time complexity for algorithms.
- Possible specifications spec include:
-
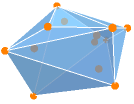
{"ConvexHull",dist,n} convex hull of n random points from the distribution dist - RandomPolyhedron[{"ConvexHull",n}] gives the convex hull of n random points from the uniform distribution UniformDistribution[3] over the unit square.
- RandomPolyhedron[spec,{k1,k2,…}] gives k1×k2×… arrays of pseudorandom polyhedra.
- RandomPolyhedron gives a different sequence of pseudorandom polyhedra whenever you run the Wolfram Language. By using SeedRandom, you can get a repeatable sequence.
- RandomPolyhedron has the same options as Polyhedron with the following additions: [List of all options]
-
DataRange Automatic the range of vertex points to generate WorkingPrecision MachinePrecision precision of vertex points - With the default setting DataRangeAutomatic, coordinates are chosen in the range 0 to 1.
-
DataRange Automatic the range of vertex points to generate VertexColors Automatic vertex colors to be interpolated VertexNormals Automatic effective vertex normals for shading VertexTextureCoordinates None coordinates for textures WorkingPrecision MachinePrecision precision of vertex points
List of all options
Examples
open allclose allBasic Examples (2)Summary of the most common use cases
Generate a random convex hull polyhedron:
Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-gzw9nf
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-m7i6no
Direct link to example
Out[2]=2
Generate a list of random polyhedra:
Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-j5sgym
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-8ltp9j
Direct link to example
Out[2]=2
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-sr2mfw
Direct link to example
Out[3]=3
Scope (4)Survey of the scope of standard use cases
Basic Uses (1)
Convex Hull Polyhedra (3)
Generate a random convex hull polyhedron:
Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-505tos
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-k3fokv
Direct link to example
Out[2]=2
Generate a list of random convex hull polyhedra:
Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-r816ep
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-uh36ku
Direct link to example
Out[2]=2
Generate a random convex hull polyhedron from the Dirichlet distribution:
Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-ugm62a
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-cqgw6
Direct link to example
Out[2]=2
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-397x37
Direct link to example
Out[3]=3
Options (2)Common values & functionality for each option
DataRange (1)
DataRange allows you to specify the range of vertex points to generate:
Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-ewpnb1
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-3k5agw
Direct link to example
Out[2]=2
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-fl0z4t
Direct link to example
Out[3]=3
Copy to clipboard.
In[4]:=4
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-fto0mi
Direct link to example
Out[4]=4
WorkingPrecision (1)
Generate a random polyhedron using machine arithmetic:
Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-rhun3x
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-t1z74c
Direct link to example
Out[2]=2
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-oj80em
Direct link to example
Out[3]=3
Copy to clipboard.
In[4]:=4
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-uzay4c
Direct link to example
Out[4]=4
Applications (3)Sample problems that can be solved with this function
Basic Uses (2)
Random polyhedra with 10 vertex points:
Copy to clipboard.
In[10]:=10
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-13y0bb
Direct link to example
Out[10]=10
Generate random polyhedra for testing algorithms and verification of time complexity:
Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-dko19g
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-i6opfi
Direct link to example
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-34otit
Direct link to example
Out[3]=3
Time complexity for algorithms for convex polyhedra:
Copy to clipboard.
In[4]:=4
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-hqm8h7
Direct link to example
Copy to clipboard.
In[5]:=5
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-oztoqj
Direct link to example
Out[5]=5
Geometry Probability (1)
Simulate random convex polyhedra and compute volumes:
Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-ncrgok
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-totrtx
Direct link to example
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-4wy34r
Direct link to example
Out[3]=3
Compare its histogram to the PDF:
Copy to clipboard.
In[4]:=4
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-edkzjq
Direct link to example
Out[4]=4
Average volume of polyhedra with 10 vertices over a unit square:
Copy to clipboard.
In[5]:=5
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-ztgkxx
Direct link to example
Out[5]=5
Properties & Relations (5)Properties of the function, and connections to other functions
Use SeedRandom to get repeatable random polyhedra:
Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-udvhjo
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-d4tuy1
Direct link to example
Out[2]=2
Use BlockRandom to block one use of RandomPolyhedron from affecting others:
Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-narvr5
Direct link to example
Out[1]=1
Use ConvexPolyhedronQ to check the property of a random polyhedron:
Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-lls03k
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-gocq6x
Direct link to example
Out[2]=2
The OuterPolyhedron of a random polyhedron is simple:
Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-nfp4bk
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-j4pdym
Direct link to example
Out[2]=2
Random polyhedra do not have voids:
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-zpe33y
Direct link to example
Out[3]=3
Using PolyhedronDecomposition to decompose a polyhedron into tetrahedra:
Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-49ud06
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-kq0zoo
Direct link to example
Out[2]=2
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hywgt6chxu48wdu-nu6nus
Direct link to example
Out[3]=3
Wolfram Research (2019), RandomPolyhedron, Wolfram Language function, https://reference.wolfram.com/language/ref/RandomPolyhedron.html.
Copy to clipboard.
✖
Wolfram Research (2019), RandomPolyhedron, Wolfram Language function, https://reference.wolfram.com/language/ref/RandomPolyhedron.html.Text
Wolfram Research (2019), RandomPolyhedron, Wolfram Language function, https://reference.wolfram.com/language/ref/RandomPolyhedron.html.
Copy to clipboard.
✖
Wolfram Research (2019), RandomPolyhedron, Wolfram Language function, https://reference.wolfram.com/language/ref/RandomPolyhedron.html.CMS
Wolfram Language. 2019. "RandomPolyhedron." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RandomPolyhedron.html.
Copy to clipboard.
✖
Wolfram Language. 2019. "RandomPolyhedron." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RandomPolyhedron.html.APA
Wolfram Language. (2019). RandomPolyhedron. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RandomPolyhedron.html
Copy to clipboard.
✖
Wolfram Language. (2019). RandomPolyhedron. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RandomPolyhedron.htmlBibTeX
Copy to clipboard.
✖
@misc{reference.wolfram_2025_randompolyhedron, author="Wolfram Research", title="{RandomPolyhedron}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/RandomPolyhedron.html}", note=[Accessed: 04-April-2025
]}BibLaTeX
Copy to clipboard.
✖
@online{reference.wolfram_2025_randompolyhedron, organization={Wolfram Research}, title={RandomPolyhedron}, year={2019}, url={https://reference.wolfram.com/language/ref/RandomPolyhedron.html}, note=[Accessed: 04-April-2025
]}