RegionHausdorffDistance

RegionHausdorffDistance[reg1,reg2]

gives the Hausdorff distance between the regions reg1 and reg2.

Details and Options

  • RegionHausdorffDistance is also known as Hausdorff metric and Pompeiu–Hausdorff distance.
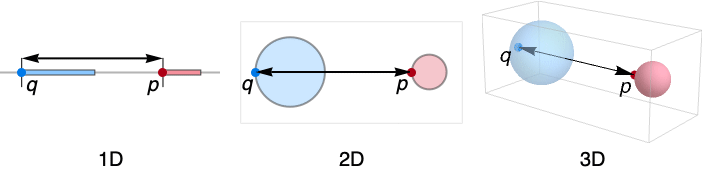
  • The Hausdorff distance measures how different two regions are from each other.
  • RegionHausdorffDistance is the greatest of all distances from a point in one region to the closest point in the other region.
  • The distance between points p and q is taken to be Norm[p-q].
  • RegionHausdorffDistance is effectively given by the maximum of MaxValue[MinValue[Norm[p-q],q∈reg2],p∈reg1] and MaxValue[MinValue[Norm[p-q],q∈reg1],p∈reg2].
  • Unless the regions are closed, the Hausdorff distance may not be attained by points in the region but in the closure of the regions.
  • The Hausdorff distance between two regions reg1 and reg2 is ϵ if reg1⊆RegionDilation[reg2,ϵ] and reg2⊆RegionDilation[reg1,ϵ].

Examples

open allclose all

Basic Examples  (4)

Find the Hausdorff distance between two disks:

Show the disks:

Find the Hausdorff distance between the unit disk and a regular polygon:

Show the regions:

Plot the Hausdorff distance as the number of sides increases:

Find the Hausdorff distance between two point clouds:

Find the Hausdorff distance between a MeshRegion and its convex hull:

Show the hull:

Scope  (9)

Special Regions  (8)

Points:

RegionHausdorffDistance accepts coordinate lists:

Lines:

Polygons:

Simplices:

Boxes:

Balls:

Spheres:

Regions in n:

Mesh Regions  (1)

The Hausdorff distance between two 1D meshes:

2D:

3D:

Options  (2)

WorkingPrecision  (2)

RegionHausdorffDistance will try to compute the distance using the same precision as its inputs:

Compute the distance using machine arithmetic:

In some cases, the exact answer cannot be computed:

Find the RegionHausdorffDistance using 30 digits of precision:

Applications  (1)

Region Reconstruction  (1)

Reconstruct a mesh from random point samples:

Determine the Hausdorff distance between the ground truth and reconstructed mesh:

Plot how the Hausdorff distance decreases with larger sample counts:

Properties & Relations  (4)

The Hausdorff distance between two points is equivalent to the EuclideanDistance:

The Hausdorff distance between two point sets is the maximum EuclideanDistance from any point to the other set:

The Hausdorff distance between a region and a single point is the furthest distance of the point to any point in the region:

RegionDistance can be used to find the nearest distance from a point to a region:

Wolfram Research (2023), RegionHausdorffDistance, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionHausdorffDistance.html.

Text

Wolfram Research (2023), RegionHausdorffDistance, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionHausdorffDistance.html.

CMS

Wolfram Language. 2023. "RegionHausdorffDistance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionHausdorffDistance.html.

APA

Wolfram Language. (2023). RegionHausdorffDistance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionHausdorffDistance.html

BibTeX

@misc{reference.wolfram_2024_regionhausdorffdistance, author="Wolfram Research", title="{RegionHausdorffDistance}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/RegionHausdorffDistance.html}", note=[Accessed: 27-April-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_regionhausdorffdistance, organization={Wolfram Research}, title={RegionHausdorffDistance}, year={2023}, url={https://reference.wolfram.com/language/ref/RegionHausdorffDistance.html}, note=[Accessed: 27-April-2024 ]}