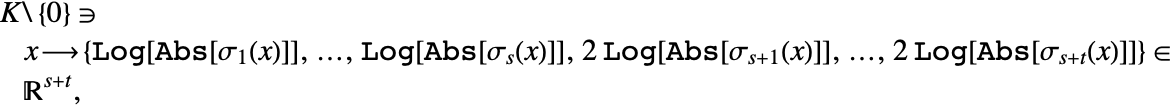Algebraic Number Fields
The Wolfram Language provides representation of algebraic numbers as Root objects. A Root object contains the minimal polynomial of the algebraic number and the root number—an integer indicating which of the roots of the minimal polynomial the Root object represents. This allows for unique representation of arbitrary complex algebraic numbers. A disadvantage is that performing arithmetic operations in this representation is quite costly. That is why the Wolfram Language requires the use of an additional function, RootReduce, in order to simplify arithmetic expressions. Restricting computations to be within a fixed finite algebraic extension of the rationals, ![]() , allows a more convenient representation of its elements as polynomials in
, allows a more convenient representation of its elements as polynomials in ![]() .
.
| AlgebraicNumber[θ,{c0,c1,…,cn}] | represent the algebraic number |
Representation of algebraic numbers as elements of a finite extension of rationals.
For any algebraic number ![]() and any list of rational numbers
and any list of rational numbers ![]() , …,
, …, ![]() , AlgebraicNumber[θ,{c0,…,cl}] evaluates to AlgebraicNumber[ξ,{d0,…,dm}], where
, AlgebraicNumber[θ,{c0,…,cl}] evaluates to AlgebraicNumber[ξ,{d0,…,dm}], where ![]() is an algebraic integer such that
is an algebraic integer such that ![]() for some factor
for some factor ![]() of the leading coefficient of the minimal polynomial of
of the leading coefficient of the minimal polynomial of ![]() ,
, ![]() is the degree of the minimal polynomial of
is the degree of the minimal polynomial of ![]() , and
, and
| ToNumberField[a,θ] | express the algebraic number a in the number field generated by θ |
| ToNumberField[{a1,a2,…},θ] | express the ai in the field generated by θ |
| ToNumberField[{a1,a2,…}] | express the ai in a common extension field generated by a single algebraic number |
Representing arbitrary algebraic numbers as elements of algebraic number fields.
Arithmetic within a fixed finite extension of rationals is much faster than arithmetic within the field of all complex algebraic numbers.
ToNumberField[{a1,a2,…}] is equivalent to ToNumberField[{a1,a2,…},Automatic], and does not necessarily use the smallest common field extension. ToNumberField[{a1,a2,…},All] always uses the smallest common field extension.
| MinimalPolynomial[a] | give a pure function representation of the minimal polynomial over the integers of the algebraic number a |
| MinimalPolynomial[a,x] | give the minimal polynomial of the algebraic number a as a polynomial in x |
| AlgebraicIntegerQ[a] | give True if the algebraic number a is an algebraic integer and False otherwise |
| AlgebraicNumberDenominator[a] | give the smallest positive integer n such that na is an algebraic integer |
| AlgebraicNumberTrace[a] | give the trace of the algebraic number a |
| AlgebraicNumberNorm[a] | give the norm of the algebraic number a |
| AlgebraicUnitQ[a] | give True if the algebraic number a is an algebraic unit and False otherwise |
| RootOfUnityQ[a] | give True if the algebraic number a is a root of unity and False otherwise |
Functions for computing algebraic number properties.
The minimal polynomial of an algebraic number ![]() is the lowest-degree polynomial
is the lowest-degree polynomial ![]() with integer coefficients and the smallest positive leading coefficient, such that
with integer coefficients and the smallest positive leading coefficient, such that ![]() .
.
An algebraic number is an algebraic integer if and only if its MinimalPolynomial is monic.
The trace of an algebraic number a is the sum of all roots of MinimalPolynomial[a].
The norm of an algebraic number a is the product of all roots of MinimalPolynomial[a].
An algebraic number ![]() is an algebraic unit if and only if both
is an algebraic unit if and only if both ![]() and
and ![]() are algebraic integers, or equivalently, if and only if AlgebraicNumberNorm[a] is
are algebraic integers, or equivalently, if and only if AlgebraicNumberNorm[a] is ![]() or
or ![]() .
.
An algebraic number ![]() is a root of unity if and only if
is a root of unity if and only if ![]() for some integer
for some integer ![]() .
.
| MinimalPolynomial[s,x,Extension->a] | |
| give the characteristic polynomial of the algebraic number s over the field | |
| MinimalPolynomial[s,x,Extension->Automatic] | |
| give the characteristic polynomial of the AlgebraicNumber object s over the number field generated by its first argument | |
| AlgebraicNumberTrace[a,Extension->θ] | |
| give the trace of the algebraic number a over the field | |
| AlgebraicNumberTrace[a,Extension->Automatic] | |
| give the trace of the AlgebraicNumber object a over the number field generated by its first argument | |
| AlgebraicNumberNorm[a,Extension->θ] | |
| give the norm of the algebraic number a over the field | |
| AlgebraicNumberNorm[a,Extension->Automatic] | |
| give the norm of the AlgebraicNumber object a over the number field generated by its first argument | |
Functions for computing properties of elements of algebraic number fields.
If a is AlgebraicNumber[θ,coeffs], then MinimalPolynomial[a,x,Extension->Automatic] is equal to MinimalPolynomial[a,x]d, where d is the extension degree of ![]() .
.
The trace of an algebraic number is the sum of all roots of its characteristic polynomial. If a is AlgebraicNumber[θ,coeffs], then AlgebraicNumberTrace[a,Extension->Automatic] is equal to d AlgebraicNumberTrace[a], where d is the extension degree of ![]() .
.
The norm of an algebraic number is the product of all roots of its characteristic polynomial. If a is AlgebraicNumber[θ,coeffs], then AlgebraicNumberNorm[a,Extension->Automatic] is equal to AlgebraicNumberNorm[a]d, where d is the extension degree of ![]() .
.
| NumberFieldIntegralBasis[a] | give an integral basis for the field |
| NumberFieldRootsOfUnity[a] | give the roots of unity for the field |
| NumberFieldFundamentalUnits[a] | give a list of fundamental units for the field |
| NumberFieldNormRepresentatives[a,m] | |
| give a list of representatives of classes of algebraic integers of norm ±m in the field | |
| NumberFieldSignature[a] | give the signature of the field |
| NumberFieldDiscriminant[a] | give the discriminant of the field |
| NumberFieldRegulator[a] | give the regulator of the field |
| NumberFieldClassNumber[a] | give the class number of a number field |
Functions of computing properties of algebraic number fields.
An integral basis of an algebraic number field ![]() is a list of algebraic numbers forming a basis of the
is a list of algebraic numbers forming a basis of the ![]() ‐module of the algebraic integers of
‐module of the algebraic integers of ![]() . The set
. The set ![]() is an integral basis of an algebraic number field
is an integral basis of an algebraic number field ![]() if and only if
if and only if ![]() are algebraic integers, and every algebraic integer
are algebraic integers, and every algebraic integer ![]() can be uniquely represented as
can be uniquely represented as
![]() is a list of fundamental units of an algebraic number field
is a list of fundamental units of an algebraic number field ![]() if and only if
if and only if ![]() are algebraic units, and every algebraic unit
are algebraic units, and every algebraic unit ![]() can be uniquely represented as
can be uniquely represented as
with a root of unity ![]() and integer exponents
and integer exponents ![]() .
.
The discriminant of a number field ![]() is the discriminant of an integral basis
is the discriminant of an integral basis ![]() of
of ![]() (i.e. the determinant of the matrix with elements AlgebraicNumberTrace[ai aj,Extension->Automatic]). The value of the determinant does not depend on the choice of integral basis.
(i.e. the determinant of the matrix with elements AlgebraicNumberTrace[ai aj,Extension->Automatic]). The value of the determinant does not depend on the choice of integral basis.
The regulator of a number field ![]() is the lattice volume of the image of the group of units of
is the lattice volume of the image of the group of units of ![]() under the logarithmic embedding
under the logarithmic embedding
where ![]() , …,
, …, ![]() are the real embeddings of
are the real embeddings of ![]() in
in ![]() , and
, and ![]() , …,
, …, ![]() are one of each conjugate pair of the complex embeddings of
are one of each conjugate pair of the complex embeddings of ![]() in
in ![]() .
.