Initial and Boundary Value Problems

Overview of Initial (IVPs) and Boundary Value Problems (BVPs)Nonlinear IVPs and BVPs
Linear IVPs and BVPsIVPs with Piecewise Coefficients

Overview of Initial (IVPs) and Boundary Value Problems (BVPs)

DSolve can be used for finding the general solution to a differential equation or system of differential equations. The general solution gives information about the structure of the complete solution space for the problem. However, in practice, one is often interested only in particular solutions that satisfy some conditions related to the area of application. These conditions are usually of two types.

  • The solution and/or its derivatives are required to have specific values at a single point, for example, and . Such problems are traditionally called initial value problems (IVPs) because the system is assumed to start evolving from the fixed initial point (in this case, 0).
  • The solution is required to have specific values at a pair of points, for example, and . These problems are known as boundary value problems (BVPs) because the points 0 and 1 are regarded as boundary points (or edges) of the domain of interest in the application.

The symbolic solution of both IVPs and BVPs requires knowledge of the general solution for the problem. The final step, in which the particular solution is obtained using the initial or boundary values, involves mostly algebraic operations, and is similar for IVPs and for BVPs.

IVPs and BVPs for linear differential equations are solved rather easily since the final algebraic step involves the solution of linear equations. However, if the underlying equations are nonlinear, the solution could have several branches, or the arbitrary constants from the general solution could occur in different arguments of transcendental functions. As a result, it is not always possible to complete the final algebraic step for nonlinear problems. Finally, if the underlying equations have piecewise (that is, discontinuous) coefficients, an IVP naturally breaks up into simpler IVPs over the regions in which the coefficients are continuous.

Linear IVPs and BVPs

To begin, consider an initial value problem for a linear first-order ODE.

This is a linear first-order ODE:
Notice that the general solution is a linear function of the arbitrary constant C[1]:
This finds a particular solution for the initial condition :
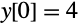
This verifies that the solution satisfies both the equation and the initial condition:
Here is the solution to the same problem with the general initial condition :
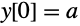
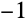
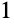
This plots several integral curves of the equation for different values of . The plot shows that the solutions have an inflection point if the parameter lies between and , while a global maximum or minimum arises for other values of :
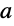
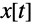
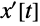
Here is the solution to a linear second-order equation with initial values prescribed for and at :
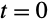
This verifies that the solution satisfies the equation and the initial conditions:
Here is a plot of the solution:
To get more information about the solutions for the problem, set :
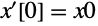
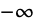
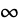
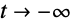
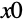
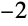
Here is a plot of the solutions for different initial directions. The solution approaches or as according to whether the value of is less than or greater than , which is the largest root of the auxiliary equation for the ODE:
Here is a BVP for an inhomogeneous linear second-order equation:

It should be noted that, in contrast to initial value problems, there are no general existence or uniqueness theorems when boundary values are prescribed, and there may be no solution in some cases.

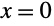
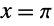
This problem has no solution because the term with C[2] in the general solution vanishes at both and . Hence there are two inconsistent conditions for the parameter C[1] and the solution is an empty set:

The previous discussion of linear equations generalizes to the case of higher-order linear ODEs and linear systems of ODEs.

Here is the solution to an Initial Value Problem (IVP) for a linear ODE of order four:
This verifies the solution and the initial conditions:
Since this is a fourth-order ODE, four independent conditions must be specified to find a particular solution for an IVP. If there is an insufficient number of conditions, the solution returned by DSolve may contain some of the arbitrary parameters, as follows:
Finally, here is the solution of an IVP for a linear system of ODEs:
This verifies that the solution satisfies the system and the initial conditions:
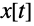
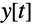
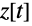
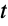
The solutions , , and are parametrized by the variable and can be plotted separately in the plane or as a curve in space:

Nonlinear IVPs and BVPs

Many real-world applications require the solution of IVPs and BVPs for nonlinear ODEs. For example, consider the logistic equation, which occurs in population dynamics.

This is the logistic equation:
The right-hand side of the equation can be expanded to a quadratic polynomial in y[t]. Hence, the logistic equation is simply a Riccati equation, and its general solution can be easily found:
This sets the intrinsic growth rate r to 1/2 and the saturation level K to 4 and solves the initial value problem:
This solves the initial value problem for the logistic equation with symbolic parameters r and K:
This verifies that the solution satisfies the equation and the initial condition:
Here is a plot of the solution for different values of r and K:
Here is an example of an IVP for a second-order nonlinear ODE whose general solution can be obtained in explicit form:
This verifies that the solution satisfies the equation and the initial conditions:
Finally, here is a boundary value problem for a nonlinear second-order ODE. The solution is required to satisfy boundary conditions at 0 and infinity. The Solve::ifun message is generated while finding the general solution in terms of JacobiSN, the inverse of EllipticF. The DSolve::bvlim messages are given because the limit required for satisfying the condition y′[Infinity]0 cannot be calculated for either branch of the general solution. However, the solution for the boundary value problem is found using an alternative method to determine the values of the constants C[1] and C[2] in the general solution:

It may not always be possible to obtain a symbolic solution to an IVP or BVP for a nonlinear equation. Numerical methods may be necessary in such cases.

IVPs with Piecewise Coefficients

The differential equations that arise in modern applications often have discontinuous coefficients. DSolve can handle a wide variety of such ODEs with piecewise coefficients. Some of the functions used in these equations are UnitStep, Max, Min, Sign, and Abs. These functions and combinations of them can be converted into Piecewise objects.

This converts the given expression into a Piecewise expression:
Here is the general solution to a first-order ODE that contains UnitStep:
Here is the solution to the same ODE with an initial condition:
The solution can be plotted in the usual way. Note that the solution is continuous but not differentiable at :
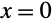
This verifies the solution:
Here is a piecewise ODE that has Max in its coefficients:

A piecewise ODE can be thought of as a collection of ODEs over disjoint intervals such that the expressions for the coefficients and the boundary conditions change from one interval to another. Thus, different intervals have different solutions, and the final solution for the ODE is obtained by patching together the solutions over the different intervals.

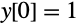
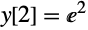
For this piecewise ODE, the expression for FinalSol is obtained by patching together SolFromMinusInfinityToTwo and SolFromTwoToInfinity. The boundary condition for the interval (-Infinity,2] is simply , while the initial condition for the interval [2,Infinity) is (given by the final value for the solution over the first interval):

If there are a large number of discontinuities in a problem, it is convenient to use Piecewise directly in the formulation of the problem.

This second-order ODE contains a Piecewise term:
This ODE contains the Clip function. The solutions are given in terms of Airy functions: