 |
OBSOLETE FOURIER SERIES PACKAGE SYMBOL
FourierCosCoefficient
As of Version 7.0, FourierCosCoefficient is part of the built-in Mathematica kernel.
gives the n
coefficient in the Fourier cosine series expansion of expr, where expr is a periodic function of t with period 1.
Details and Options
- To use
, you first need to load the Fourier Series Package using Needs["FourierSeries`"]. - The n
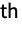coefficient in the Fourier cosine series expansion of expr is by default defined to be 2Integrate[expr Cos[2
n t], {t, -
, 
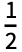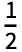}] for n>0 and Integrate[expr, {t, -
, 
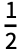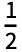}] for n==0. - If n is numeric, it should be an explicit integer.
- Different choices for the definition of the Fourier cosine series expansion can be specified using the option FourierParameters.
- With the setting FourierParameters->{a, b}, expr is assumed to have a period of
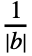, and the n
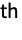coefficient computed by 
is 2
b
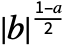Integrate[expr Cos[2 b n t], {t, -
, 
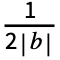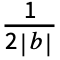}] for n>0 and b
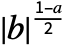Integrate[expr, {t, -
, 
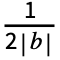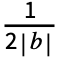}] for n==0. - In addition to the option FourierParameters,
can also accept the options available to Integrate. These options are passed directly to Integrate.
