Getting Started

The Wolfram Language comes with all the tools and configurations that allow you to immediately carry out parallel computing. Note that to take advantage of parallel computing, it is often better to have a multicore machine or access to a grid of parallel Wolfram Language kernels. Luckily, multicore machines have been common in many types of configurations for some time.

A first step that may just demonstrate that the system is running is a ParallelEvaluate. If this is the first parallel computation, it will launch the configured parallel kernels.

The following example should return the process ID for each parallel kernel.

This returns the machine name for each kernel; it shows that everything is running on the same computer.

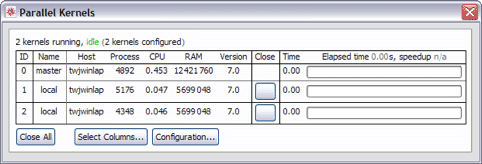
You might find it useful to open the Parallel Kernels Status monitor, which looks something like the following.

Now you can carry out an actual computation. One very simple type of parallel program is to do a search. In the following example, one is added to a factorial and the result is tested to see if it is a prime number. This is done by wrapping the regular Wolfram Language computation in Parallelize.

This shows us that some of these numbers are prime.

Another example is to look for Mersenne prime numbers. This is done with the following, again wrapping the computation in Parallelize.

This shows that the first 15 Mersenne prime numbers have been found.

When you get to this stage, you should be ready to start carrying out parallel computation in the Wolfram Language.

Using Your Own Functions in Parallel Computations

The previous example worked by simply wrapping a parallelizable expression in Parallelize[…]. If the expressions involve not only built-in functions, but functions you defined yourself, some preparatory work is necessary.

Definitions for symbols to be evaluated on the parallel kernels, other than built-in ones, need to be distributed to all kernels before they can be used.

Define a predicate that tests whether

is prime.

Distribute the definition to all parallel kernels.

Now it can be used as part of a parallel computation.

What happens if you forget to distribute definitions for a parallel computation?

This definition is the same as mersenneQ above.

The parallel kernels do not know the definition, so it never returns True.

In many cases the computation seems to work anyway, but if you analyze its performance, you should see that it was not in fact evaluated as fast as it should have been.

This computation gives the right result, but it is not faster than a normal Table would be.

The reason it seems to work is that the unknown function m2 does not evaluate on the parallel kernels, so the expressions m2[10000], m2[10001], … are sent back, and they then evaluate on the master kernel, where the definition is known.

Top