MATHEMATICA FEATURED EXAMPLE
Tensor Canonicalization
Mathematica includes a powerful tensor canonicalizer, which can bring expressions involving products, contractions, and transpositions of tensors with symmetries into a standard form. From these standard forms, computations can be optimized, and new identities can be derived.
Declare
to be a rank-4 tensor in dimension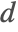
with the transposition symmetries of the Riemann tensor:
There are more than 40,000 possible contractions of
, but this counts each contraction multiple times due to contraction order. Accounting for order, there are 105 possible complete contractions:
| Out[16]= |  |
However, due to symmetry, there are only nine possible results, and five if the sign is ignored:
| Out[17]= |  |
The canonicalizer uses state-of-the-art algorithms to return answers quickly. It can process all 40,320 raw contractions in less than a minute:
| Out[18]= |  |
