 |
BUILT-IN MATHEMATICA SYMBOL
BSplineSurface
BSplineSurface[array]
is a graphics primitive that represents a non-uniform rational B-spline surface defined by an array of 
control points.
Details and Options
- BSplineSurface can be used in Graphics3D (three-dimensional graphics).
- The positions of control points can be specified either in ordinary coordinates as
, or in scaled coordinates as Scaled[{x, y, z}]. - The following options can be given:
-
SplineDegree Automatic degree of polynomial basis SplineKnots Automatic knot sequence in each dimension SplineWeights Automatic control point weights SplineClosed False whether to make the surface closed - By default, BSplineSurface uses bicubic splines, corresponding to degree
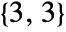. - The option SplineDegree->d specifies maximal degree d in each direction. SplineDegree->{d1, d2} specifies different maximal degrees in the two directions within the surface.
- By default, knots are chosen to be uniform and to make the surface reach the control points at the edges of the array.
- SplineKnots->{list1, list2} specifies sequences of knots to use for the rows and columns of the array of control points.
- With an explicit setting for SplineKnots, the degree of the polynomial basis is determined from the number of knots specified and the number of control points.
- SplineWeights are automatically chosen to be 1, corresponding to a polynomial B-spline surface.
- FaceForm and EdgeForm can be used to specify how the interiors and boundaries of BSplineSurface objects should be rendered.
- You can use graphics directives such as GrayLevel, RGBColor, and Opacity to specify how BSplineSurface objects should be rendered.
- You can specify surface material properties using the graphics directives Specularity and Opacity.
- You can use FaceForm[front, back] to specify different properties for front and back faces.
- Individual coordinates and lists of coordinates in BSplineSurface can be Dynamic objects.
New in 7
