BUILT-IN MATHEMATICA SYMBOL

ChanVeseBinarize

ChanVeseBinarize[image]
finds a two-level segmentation of image by computing optimal contours around regions of consistent intensity in image.

ChanVeseBinarize[image, marker]
uses the foreground pixels of marker as the initial contours.

Details and Options Details and Options

ChanVeseBinarize implements an iterative active contour method to achieve a two-level segmentation of an image.
ChanVeseBinarize works with arbitrary grayscale and multichannel images.
In ChanVeseBinarize[image, marker], marker can be given either as an image, a graphics object, or a list of points in the standard image coordinate system, where x runs from 0 to width and y runs from 0 to height, and position corresponds to the bottom-left corner of the image.
ChanVeseBinarize uses the Euclidean distance between channel vectors to determine the similarity between pixels inside and outside of the contour.
ChanVeseBinarize iteratively minimizes a functional that is a weighted sum of the contour length, the enclosed area, and the deviation between the image and the two-level segmentation.
The weights can be specified with the following options:

"AreaPenalty"	0	penalty associated with the area enclosed by the contour
"LengthPenalty"	0.03	contour length penalty
"LevelPenalty"	{1.0,1.0}	penalties for the total pixel deviations in the two segments
"TargetColor"	Automatic	target foreground color

With the setting , both foreground and background colors can be specified.
The maximum number of iteration steps is given by the MaxIterations option with default setting 100.
The Chan-Vese segmentation of an image domain 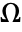into the two segments 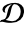and 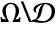with contour 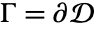minimizes the following functional 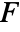of image :
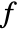$F(c_1,c_2,Gamma)=mu Length[Gamma]+nu Area(D)+lambda_1int_DTemplateBox[{{f, -, {c, _, 1}}}, Abs]^2dxdy+lambda_2int_(Omega\D)TemplateBox[{{f, -, {c, _, 2}}}, Abs]^2dxdy$
The Chan-Vese functional is parametrized by the length penalty 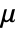, the area penalty 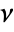, and level penalties 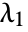and .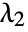
The Chan-Vese algorithm partitions image such that the first segment 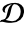will differ as little as possible from constant 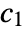and the second segment 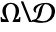will deviate as little as possible from constant 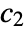. If constants 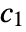and 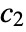are not specified, one assumes c₁=Mean[f] in 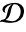, and c₂=Mean[f] in .
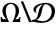The contour 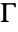between the two resulting segments 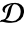and 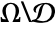will exhibit a short length for 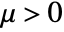, and for 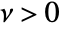the area of 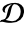will tend to be small or for tend to be large.
The weighting coefficients , , , and are accessible through the following options.
ChanVeseBinarize works with Image3D objects.