BUILT-IN MATHEMATICA SYMBOL

CurvatureFlowFilter

CurvatureFlowFilter[image]
applies a mean curvature flow filter to image.

CurvatureFlowFilter[image, t]
specifies the amount t of curvature flow to be applied.

CurvatureFlowFilter[image, t, k]
applies the curvature flow with a modified conductance term parametrized by k.

Details Details

Curvature flow filtering is an anisotropic diffusion method used for smoothing images while preserving edges. It effectively spreads the curvature along a contour, thereby rounding corners and reducing the Euclidean length of contours.
CurvatureFlowFilter implements a Euclidean shortening filter.
CurvatureFlowFilter works on arbitrary grayscale or multichannel images, operating on each channel separately.
The diffusion in a curvature flow filter runs parallel to the image contours. Diffusion perpendicular to the contours is omitted in order to preserve edges.
The effect of CurvatureFlowFilter does not depend on the overall normalization of the image values.
The conductance parameter k can take any positive value. The default value k=∞ renders the unmodified curvature flow filter.
CurvatureFlowFilter[image] is equivalent to CurvatureFlowFilter[image, 1, Infinity].
applies the partial differential equation $partial_tf=kappa TemplateBox[{{del , f}}, Abs]$ with the contour curvature to every image channel .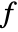
In CurvatureFlowFilter[image, t], t parametrizes the evolution of the curvature flow and thereby the spatial range of the filter.
If a parameter k is supplied, the curvature flow $partial_tf=TemplateBox[{{del , f}}, Abs]del .c_k(TemplateBox[{{del , f}}, Abs]) (del f)/(TemplateBox[{{del , f}}, Abs])$ with a modified conductance term $c_k(TemplateBox[{{del , f}}, Abs])=ⅇ^(-|del f|^2/k^2)$ is used.