Search for all pages containing FiniteGroupData
-
See Also
- FiniteGroupCount
- FiniteAbelianGroupCount
- GraphData
- LatticeData
-
- Entity Types
- FiniteGroup
-
- Interpreter Types
- FiniteGroup
- ComputedFiniteGroup
- Related Guides
FiniteGroupData[name,"property"]
gives the value of the specified property for the finite group specified by name.
FiniteGroupData["class"]
gives a list of finite groups in the specified class.


FiniteGroupData
FiniteGroupData[name,"property"]
gives the value of the specified property for the finite group specified by name.
FiniteGroupData["class"]
gives a list of finite groups in the specified class.
Details












- Groups can be specified by names such as "C3", "Quaternion", and {"SymmetricGroup",4}.
- FiniteGroupData[name] gives the standard form of the name for the group specified by name.
- FiniteGroupData[patt] gives a list of all group names that match the string pattern patt.
- FiniteGroupData[] and FiniteGroupData[All] give a list of available named finite groups, such as "Quaternion", and small members of infinite families, such as the first 10 members of {"SymmetricGroup",deg}. FiniteGroupData can work with other members of those infinite families.
- FiniteGroupData[{n, id},…] gives data for the finite group of order n with identifier id.
- FiniteGroupData[n] gives a list of nonisomorphic finite groups of order n.
- FiniteGroupData[;;n] gives a list of nonisomorphic groups with orders up to n.
- FiniteGroupData[n1;;n2] gives a list of nonisomorphic groups of order n1 through n2.
- FiniteGroupData[{"type", id}, …] gives data for the finite group of the specified type with identifier id. The identifier is typically an integer or a list of integers.
- Fundamental families of groups include:
-
{"AlternatingGroup",n} alternating group 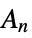
{"CrystallographicPointGroup",n} three-dimensional crystallographic point group, 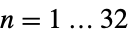
{"CyclicGroup",n} cyclic group 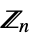
{"CyclicGroupUnits",n} units group 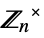 of the cyclic group
of the cyclic group{"DicyclicGroup",n} dicyclic group 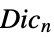
{"DihedralGroup",n} dihedral group 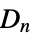
{"PointGroup",id} three-dimensional point groups {"SymmetricGroup",n} symmetric group 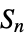
- Finite simple groups include:
-
{"ProjectiveSpecialLinearGroup",{n,q}} projective special linear group 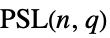
{"ProjectiveSymplecticGroup",{n,q}} projective symplectic group 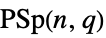
{"ChevalleyGroupB",{n,q}} exceptional Chevalley group 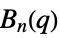
{"ChevalleyGroupD",{n,q}} exceptional Chevalley group 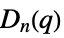
{"ChevalleyGroupE",{n,q}} exceptional Chevalley group 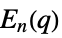 ,
, 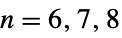
{"ChevalleyGroupF",{4,q}} exceptional Chevalley group 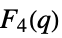
{"ChevalleyGroupG",{2,q}} exceptional Chevalley group 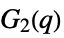
{"ReeGroupF",q} Ree group 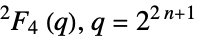
{"ReeGroupG",q} Ree group 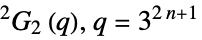
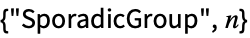
sporadic simple group, 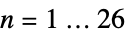
{"SteinbergGroupA",{n,q}} Steinberg unitary group 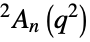
{"SteinbergGroupD",{n,q}} Steinberg orthogonal group 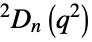
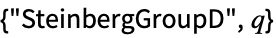
Steinberg orthogonal group 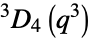
{"SteinbergGroupE",q} Steinberg orthogonal group 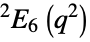

Suzuki group 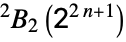
- Special group specifications include:
-
{"AbelianGroup",{m,n,…}} Abelian group 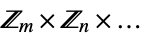
{"DirectProduct",{group1,group2,…}} direct product of groups {"SemidirectProduct",{group1,group2}} semi-direct product 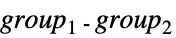 , with
, with 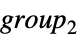 normal in the result
normal in the result - FiniteGroupData["Properties"] gives a list of properties available for groups.
- Basic group properties include:
-
"Center" center of group (subgroup of commuting elements) "CenterElements" elements of the center subgroup "ClassNumber" class number "CommutatorSubgroup" commutator subgroup "CommutatorSubgroupElements" elements of the commutator subgroup "ConjugacyClasses" conjugacy classes "ElementNames" list of names of elements "Elements" elements of group "Exponent" exponent of group "Generators" generator elements "InverseGenerators" inverses of the generator elements "Inverses" inverse elements "MultiplicationTable" multiplication table "NormalSubgroupElements" elements of normal subgroups "NormalSubgroups" normal subgroups "Order" total number of elements "SubgroupElements" elements of subgroups "Subgroups" subgroups "SylowSubgroupCounts" sizes of the Sylow subgroups "SylowSubgroupElements" elements of the Sylow subgroups "SylowSubgroups" 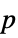 -Sylow subgroups
-Sylow subgroups - The elements of a group are specified by integers running from 1 to the order of the group, with 1 corresponding to the identity element.
- Group structure properties include:
-
"AutomorphismGroup" automorphism group "InnerAutomorphismGroup" inner automorphism group "IsomorphicGroups" list of isomorphic groups "OuterAutomorphismGroup" outer automorphism group "QuotientGroups" list of quotient groups "SchurMultiplier" Schur multiplier - Permutation group properties include:
-
"CycleIndex" cycle index "Cycles" cycles "PermutationRepresentation" representation as permutation lists "PermutationGroupRepresentation" representation as a Wolfram System permutation group "Transitivity" transitivity level - Other properties include:
-
"DefiningRelations" relations that describe the group algebra "CayleyGraph" Cayley graph for the built-in choice of generators "Classes" classes to which the group belongs "CycleGraph" cycle graph "Information" information about group "ParameterRange" assumptions on parameters - Group representation properties include:
-
"CharacterTable" group element characters "ConjugacyClassNames" names of conjugacy classes "ConjugacyClassSizes" sizes of conjugacy classes "MatrixRepresentation" representation as matrices "RepresentationDimensions" dimensions of the representations "RepresentationNames" names of the representations "SpaceRepresentation" representation as 3D Cartesian coordinate transformations - Additional properties for crystallographic point groups include:
-
"BravaisLattices" compatible Bravais lattices "CrystalForm" crystal form "CrystalSystem" crystal system "HermannMauguin" Hermann–Mauguin notation "Orbifold" orbifold notation "PointGroupType" point group type "Schoenflies" Schoenflies notation "Shubnikov" Shubnikov notation - FiniteGroupData["Classes"] gives a list of all supported classes.
- FiniteGroupData[name,"Classes"] gives a list of all the classes the specified group is in.
- FiniteGroupData[name,"class"] gives True or False depending on whether a group corresponding to name is in the specified class.
- FiniteGroupData["class"] gives the list of finite groups in FiniteGroupData[] belonging to the specified class.
- FiniteGroupData["class",n] gives a list of finite groups of order n in the specified class.
- FiniteGroupData["class",;;n] gives a list of finite groups of order less than or equal to n in the specified class.
- FiniteGroupData["class",n;;] gives a list of finite groups of order greater than or equal to n in the specified class.
- FiniteGroupData["class",n1;;n2] gives a list of finite groups of order greater than n1 and less than n2 in the specified class.
- Classes of groups include:
-
"Abelian" Abelian "Alternating" alternating "Cyclic" cyclic "Dihedral" dihedral "Perfect" perfect "Simple" simple "Solvable" solvable "Sporadic" sporadic "Symmetric" symmetric "Transitive" transitive - Negative classes of groups include:
-
"Nonabelian" not Abelian "Nonalternating" not alternating "Noncyclic" not cyclic "Nondihedral" not dihedral "Nonperfect" not perfect "Nonsimple" not simple "Nonsolvable" not solvable "Nonsporadic" not sporadic "Nonsymmetric" not symmetric "Nontransitive" not transitive - A group belongs to the classes "Alternating", "Cyclic", "Dihedral" or "Symmetric" if it is isomorphic to the alternating, cyclic, dihedral or symmetric group of the same order, respectively.
- A group belongs to the class "Transitive" if the corresponding permutation representation provided is transitive. The permutation representation for {"DirectProduct",{group1,group2,…}} is constructed on the disjoint union of the respective domains of action of the factor groups, and hence it is not transitive.
- Naming-related properties include:
-
"AlternateNames" alternate English names, as strings "AlternateStandardNames" alternate standard Wolfram Language names "Name" English name as a string "Notation" group notation "ShortName" short name as a string "StandardName" standard Wolfram Language name - FiniteGroupData[name,"Information"] gives a hyperlink to additional information on the specified group.
- Using FiniteGroupData may require internet connectivity.
Examples
open all close allScope (34)
Names and Classes (6)
A list of all named finite groups and small members of infinite families, many of them mutually isomorphic:
Finite groups whose standard name is a string:
Find the English name of a finite group:
A list of alternate names can also be found:
Some groups can be given in shorter form:
List of the groups in FiniteGroupData[] belonging to a given class:
Test membership of a group in the class:
Restrict the members of a class to a given order. These are all mutually isomorphic groups:
The list of 26 simple sporadic groups:
Short forms of the 3-dimensional crystallographic point groups:
FiniteGroupData[n] returns a list of non-isomorphic groups of order n, first having the Abelian groups and then the non-Abelian groups:
When FiniteGroupData does not have a named version of a given group, it is specified as {order,index}:
Properties and Annotations (4)
Property Values (3)
Detailed Properties (21)
Names & Notations (3)
In general, groups are referred to by standard name:
That is equivalent to this simpler syntax:
Other acceptable forms of input are called alternate standard names:
This is the English name for a group, always a string:
Some groups have alternate names:
There is also a short string form of the name:
Every group has a short notation form:
The default notation for the 32 three-dimensional crystallographic point groups is Schoenflies notation, but other notations are possible:
Basic Group Properties (4)
Two important properties of a group are its order and multiplication table:
The multiplication table defines the group as an abstract group (that is, up to isomorphism). For example, the group is Abelian if and only if its multiplication table is symmetric:
The elements of the group are abstractly identified by their position in the multiplication table:
This allows identification of which elements form the various subgroups. For example, the fourth element commutes with all other group elements:
More information on the commutativity of a group is given by the group of all commutators in the group. This group is not Abelian because the commutator (or derived) subgroup is not trivial:
However, upon further commutation we get the trivial group:
Hence, the original group is solvable:
These are the cycles obtained by repeated multiplication of each element with itself:
They have a natural representation as a graph. The identity element is highlighted:
Group Representations (4)
Presentations in terms of generators and relations:
The group product is represented as a small circle, also used to denote its associated power:
With those two generators (of respective orders 4 and 2) we have this Cayley graph:
Naming the generators, it is possible to give all elements of the groups as words:
Permutation group representations as the complete set of permutation lists:
Or as a permutation group that can be used for further computation:
It is a transitive representation, because it has a single orbit:
However, any stabilizer is trivial:
Hence, this is not a multiply-transitive representation:
The cyclic structure of a permutation representation gives the so-called cycle index polynomial:
Group Isomorphism (1)
Group Structure (8)
Conjugacy classes of a group, given as respective lists of elements:
The class number is defined as the number of conjugacy classes:
Those elements that are self-conjugate, hence commuting with all other elements in the group, form the center of that group:
The Klein 4-group only has one type of proper subgroup:
But that type is realized three times:
For n≥5 the alternating groups ![]() are equal to their commutator subgroups:
are equal to their commutator subgroups:
Groups with such property are called perfect:
All simple groups are perfect:
Normal subgroups of the "Tetrahedral" group:
It has nontrivial normal subgroups, and therefore it is not simple:
Sylow subgroups are those whose order is a maximal power of a prime:
Possible quotient groups, obtained by finding the quotient with respect to normal subgroups:
Generalizations & Extensions (2)
Find the list of group names matching a pattern:
Some properties are available for symbolic parameters in infinite families of groups:
This is the valid range of values for the parameter:
However, most properties require integer values for such parameters. In those cases Missing["NotApplicable"] is returned:
Properties & Relations (3)
FiniteGroupCount[n] gives the number of finite groups of order n:
Consistently, when address by order, FiniteGroupData returns a list of non-isomorphic groups:
Obtain other groups isomorphic to those:
FiniteAbelianGroupCount[n] gives the number of Abelian groups of order n:
All finite groups of order 1225 are Abelian:
The group of units of the ring of integers modulo n is always Abelian, but not always cyclic:
A group is cyclic if there is an element whose order is the group order. The order of {"CyclicGroupUnits", n} is EulerPhi[n], while CarmichaelLambda[n] gives the maximum order amongst its elements.
For example, the following group is cyclic because there are elements whose order is the group order:
The condition EulerPhi[n]CarmichaelLambda[n] is only obeyed for positive integers n of the form 2, 4, pk, 2pk with prime p≠2 and k≥1.
Possible Issues (1)
Results from FiniteGroupData may contain isomorphic groups:
There is only one group of order 1:
Using the order as first argument guarantees non-isomorphic results:
See Also
FiniteGroupCount FiniteAbelianGroupCount GraphData LatticeData
Entity Types: FiniteGroup
Interpreter Types: FiniteGroup ComputedFiniteGroup
Related Guides
Related Links
History
Introduced in 2008 (7.0) | Updated in 2012 (9.0) ▪ 2020 (12.1)
Text
Wolfram Research (2008), FiniteGroupData, Wolfram Language function, https://reference.wolfram.com/language/ref/FiniteGroupData.html (updated 2020).
CMS
Wolfram Language. 2008. "FiniteGroupData." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/FiniteGroupData.html.
APA
Wolfram Language. (2008). FiniteGroupData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FiniteGroupData.html
BibTeX
@misc{reference.wolfram_2025_finitegroupdata, author="Wolfram Research", title="{FiniteGroupData}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FiniteGroupData.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_finitegroupdata, organization={Wolfram Research}, title={FiniteGroupData}, year={2020}, url={https://reference.wolfram.com/language/ref/FiniteGroupData.html}, note=[Accessed: 06-February-2026]}