 |
BUILT-IN MATHEMATICA SYMBOL
FourierCosCoefficient
FourierCosCoefficient[expr, t, n]
gives the n
coefficient in the Fourier cosine series expansion of expr.
FourierCosCoefficient[expr, {t1, t2, ...}, {n1, n2, ...}]
gives a multidimensional Fourier cosine coefficient.
Details and Options
- The
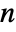
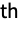coefficient in the Fourier cosine series expansion of 
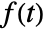is by default given by 
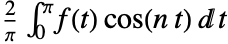. - The
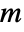-dimensional Fourier cosine coefficient is given by 
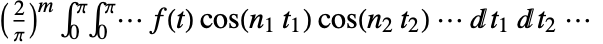. - In the form FourierCosCoefficient[expr, t, n], n can be symbolic or a non-negative integer.
- The following options can be given:
-
Assumptions $Assumptions assumptions on parameters FourierParameters {1,1} parameters to define Fourier series GenerateConditions False whether to generate results that involve conditions on parameters - The function expr is assumed to be periodic in t with period
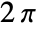, except when otherwise specified by FourierParameters. - Common settings for FourierParameters include:
-
{1,1}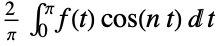 
default settings {1,2Pi}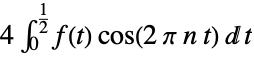 
period 1 {a,b}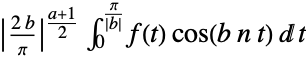 
general setting
Fourier cosine coefficient:
New in 7
