WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

JordanModelDecomposition
✖
JordanModelDecomposition

✖

yields the Jordan decomposition of the state-space model ssm.

Details

  • The result is a list {p,jc}, where p is a similarity matrix, and jc is the Jordan canonical form of ssm.
  • The state-space model ssm can be given as StateSpaceModel[{a,b,c,d}], where a, b, c, and d represent the state, input, output, and transmission matrices in either a continuous-time or a discrete-time system:
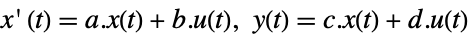
  • continuous-time system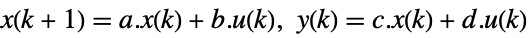
    discrete-time system
  • The transformation 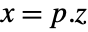, where 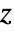is the new state vector, and 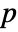is a similarity matrix that spans the linearly independent eigenvectors of 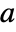, transforms the system into the Jordan canonical form:
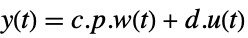
  • w'(t)=TemplateBox[{p}, Inverse].a.p.w(t)+TemplateBox[{p}, Inverse].b.u(t), continuous-time system
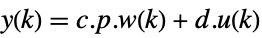    w(k+1)=TemplateBox[{p}, Inverse].a.p.w(k)+TemplateBox[{p}, Inverse].b.u(k),.discrete-time system
  • The new state matrix TemplateBox[{p}, Inverse].a.p is the Jordan canonical form of the old state matrix .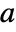

Examples

open allclose all

Basic Examples  (1)Summary of the most common use cases

Compute the Jordan decomposition of a state-space model:

In[1]:=1
✖
https://wolfram.com/xid/0elxzkop2oiejki-6jueqr
Out[1]=1

Scope  (4)Survey of the scope of standard use cases

The Jordan decomposition of a second-order system:

In[1]:=1
✖
https://wolfram.com/xid/0elxzkop2oiejki-c9pau9
Out[1]=1

The Jordan decomposition of a discrete-time system:

In[1]:=1
✖
https://wolfram.com/xid/0elxzkop2oiejki-31wjnw
Out[1]=1

A transformation that gives the complex poles in second-order blocks:

In[1]:=1
✖
https://wolfram.com/xid/0elxzkop2oiejki-yosrty
Out[1]=1

Repeated poles appear in Jordan blocks:

In[1]:=1
✖
https://wolfram.com/xid/0elxzkop2oiejki-relxjc
Out[1]=1

Applications  (2)Sample problems that can be solved with this function

A system is controllable if and only if the Jordan blocks of have distinct eigenvalues, and the row of corresponding to the last row of each Jordan block is not zero:

In[1]:=1
✖
https://wolfram.com/xid/0elxzkop2oiejki-mdatow
In[2]:=2
✖
https://wolfram.com/xid/0elxzkop2oiejki-8isw0h
Out[2]=2

A system is observable if and only if the Jordan blocks of have distinct eigenvalues, and the column of corresponding to the first row of each Jordan block is not zero:

In[1]:=1
✖
https://wolfram.com/xid/0elxzkop2oiejki-8txb24
In[2]:=2
✖
https://wolfram.com/xid/0elxzkop2oiejki-nau8o6
Out[2]=2

Properties & Relations  (3)Properties of the function, and connections to other functions

In the Jordan canonical form, the eigenvalues are along the diagonal of the state matrix:

In[1]:=1
✖
https://wolfram.com/xid/0elxzkop2oiejki-rf2g5o
In[2]:=2
✖
https://wolfram.com/xid/0elxzkop2oiejki-ffwwis
In[3]:=3
✖
https://wolfram.com/xid/0elxzkop2oiejki-uzm6cz
Out[3]=3

The Jordan canonical form is related to the original system via the similarity transform:

In[1]:=1
✖
https://wolfram.com/xid/0elxzkop2oiejki-70qbc4
In[2]:=2
✖
https://wolfram.com/xid/0elxzkop2oiejki-7o7w1s
In[3]:=3
✖
https://wolfram.com/xid/0elxzkop2oiejki-f8dzgk
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0elxzkop2oiejki-xly1jf
Out[4]=4

The Jordan canonical form of a state-space model is the similarity transformation associated with the Jordan decomposition of its state matrix:

In[1]:=1
✖
https://wolfram.com/xid/0elxzkop2oiejki-l4sreh
In[2]:=2
✖
https://wolfram.com/xid/0elxzkop2oiejki-w21m1l
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0elxzkop2oiejki-325cm4
Out[3]=3

Possible Issues  (1)Common pitfalls and unexpected behavior

JordanModelDecomposition does not support descriptor systems:

In[1]:=1
✖
https://wolfram.com/xid/0elxzkop2oiejki-jglyz
Out[1]=1

Use KroneckerModelDecomposition to separate the modes of the system:

In[3]:=3
✖
https://wolfram.com/xid/0elxzkop2oiejki-gvdcit
Out[3]=3
Wolfram Research (2010), JordanModelDecomposition, Wolfram Language function, https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.
✖
Wolfram Research (2010), JordanModelDecomposition, Wolfram Language function, https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.

Text

Wolfram Research (2010), JordanModelDecomposition, Wolfram Language function, https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.

✖
Wolfram Research (2010), JordanModelDecomposition, Wolfram Language function, https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.

CMS

Wolfram Language. 2010. "JordanModelDecomposition." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.

✖
Wolfram Language. 2010. "JordanModelDecomposition." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.

APA

Wolfram Language. (2010). JordanModelDecomposition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JordanModelDecomposition.html

✖
Wolfram Language. (2010). JordanModelDecomposition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JordanModelDecomposition.html

BibTeX

@misc{reference.wolfram_2025_jordanmodeldecomposition, author="Wolfram Research", title="{JordanModelDecomposition}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/JordanModelDecomposition.html}", note=[Accessed: 30-March-2025 ]}

✖
@misc{reference.wolfram_2025_jordanmodeldecomposition, author="Wolfram Research", title="{JordanModelDecomposition}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/JordanModelDecomposition.html}", note=[Accessed: 30-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_jordanmodeldecomposition, organization={Wolfram Research}, title={JordanModelDecomposition}, year={2010}, url={https://reference.wolfram.com/language/ref/JordanModelDecomposition.html}, note=[Accessed: 30-March-2025 ]}

✖
@online{reference.wolfram_2025_jordanmodeldecomposition, organization={Wolfram Research}, title={JordanModelDecomposition}, year={2010}, url={https://reference.wolfram.com/language/ref/JordanModelDecomposition.html}, note=[Accessed: 30-March-2025 ]}