Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Wolfram Language & System Documentation Center

KroneckerModelDecomposition

KroneckerModelDecomposition

KroneckerModelDecomposition[ssm]

yields the Kronecker decomposition of a descriptor state-space model ssm.

Details and Options

The Kronecker decomposition is also known as the Weierstrass decomposition.
The result is a list {{p,q},kssm}, where p and q are transformation matrices, and kssm is the Kronecker form of ssm.
The decomposition decouples a descriptor state-space model into slow and fast subsystems.
The slow subsystem has the same form as a standard state-space model with state equation:
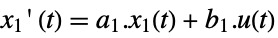
continuous time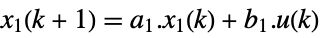

discrete time
The fast subsystem is governed by the following state equations where e₂ is nilpotent:
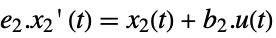
continuous time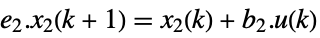

discrete time
The output of the system in Kronecker form is:
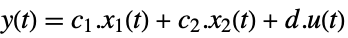
continuous time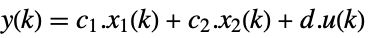

discrete time
The matrices a₁ and e₂ are both taken to be in Jordan form.
StateSpaceTransform[ssm,{p,q}] has the form StateSpaceModel[{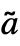,,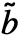,,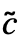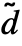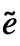}], with 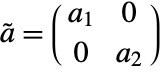and 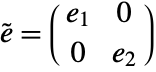, where 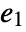and a₂ are identity matrices with the dimensions of the slow and fast subsystems, and 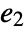is a nilpotent matrix.

Examples

open all close all

Basic Examples (1)

Compute the Kronecker decomposition of a state-space model:

Scope (4)

The Kronecker decomposition of a system with two fast states and two slow states:

The Kronecker decomposition of a discrete-time system:

An algebraic system:

An impulsive system:

Applications (2)

KroneckerModelDecomposition decouples the fast and slow subsystems:

The number of 1s on the diagonal of the descriptor matrix gives the number of slow states:

Separate the slow and fast systems using SystemsModelExtract and SystemsModelDelete:

An RLC circuit modeled as a descriptor state space:

Properties & Relations (6)

The Kronecker decomposition and the original system are restricted equivalent systems:

They have the same order:

They have the same controllability and observability properties:

They have the same transfer functions:

Nonsingular systems give an identity matrix for the descriptor matrix:

Find the Kronecker decomposition of a singular descriptor state-space model:

The matrix pair {p,q} relates the original system to the Kronecker form:

The inverse matrices perform the opposite transformation:

The slow and fast subsystems model the proper and improper parts of a transfer function:

The state matrix in the slow subsystem is in Jordan form:

The descriptor matrix in the fast subsystem is in Jordan form with all zero eigenvalues:

Top