MomentConvert

MomentConvert[mexpr,form]

converts the moment expression mexpr to the specified form.

Details

  • MomentConvert handles both formal moment and formal sample moment expressions.
  • A formal moment expression can be any polynomial in formal moments of the form:
  • Moment[r]formal r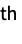^(th) moment
    CentralMoment[r]formal r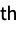^(th) central moment
    FactorialMoment[r]formal r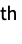^(th) factorial moment
    Cumulant[r]formal r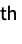^(th) cumulant
  • Formal moment expressions can be evaluated for any particular distribution using MomentEvaluate.
  • A moment expression can be converted into any other moment expression.
  • The following forms can used for converting between moment expressions:
  • "Moment"convert to formal moments
    "CentralMoment"convert to formal central moments
    "FactorialMoment"convert to formal factorial moments
    "Cumulant"convert to formal cumulants
  • A sample moment expression is any polynomial in formal symmetric polynomials of the form:
  • PowerSymmetricPolynomial[r]formal r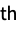^(th) power symmetric polynomial
    AugmentedSymmetricPolynomial[{r1,r2,…}]formal {r1,r2,…} augmented symmetric polynomial
  • Sample moment expressions can be evaluated on a dataset using MomentEvaluate.
  • A sample moment expression can be converted into any other sample moment expression.
  • The following forms can used for converting between sample moment expressions:
  • "PowerSymmetricPolynomial"convert to formal power symmetric polynomial
    "AugmentedSymmetricPolynomial"convert to formal augmented symmetric polynomial
  • Sample moment expressions are effectively moment estimators assuming independent, identically distributed samples.
  • Moment estimators for a given moment expression can be constructed using the forms:
  • "SampleEstimator"construct a sample moment estimator
    "UnbiasedSampleEstimator"construct an unbiased sample moment estimator
  • Sample moment expressions can be considered a random variable constructed from independent, identically distributed random variables. The expected value can be found by converting from its sample moment expression to a moment expression.
  • The expectation for a given sample moment expression can be computed using the forms:
  • "Moment"express in terms of formal moments
    "CentralMoment"express in terms of formal central moments
    "FactorialMoment"express in terms of formal factorial moments
    "Cumulant"express in terms of formal cumulants
  • MomentConvert[expr,form1,form2,…] first converts to form1, then to form2, etc.

Examples

open allclose all

Basic Examples  (2)

Express the cumulant in terms of raw moments:

Express the multivariate cumulant in terms of central moments:

Find an unbiased sample estimator for the second cumulant, i.e. second k-statistics:

Convert the estimator to the basis of power symmetric polynomials:

Compute expectation of the estimator in terms of raw moments:

Scope  (4)

Express a multivariate cumulant in terms of raw moments:

Convert back to the cumulant:

Find an unbiased sample estimator for a product of univariate central moments, also known as polyache:

Find a multivariate polyache:

Find the sampling distribution estimator expectation of an augmented symmetric polynomial:

Convert the augmented symmetric polynomial to the basis of power symmetric polynomials:

Evaluate at a sample of size 3:

Compare to direct evaluation of the augmented symmetric polynomial:

Generalizations & Extensions  (2)

Find the h-statistic in basis of power symmetric polynomials:

Find the sampling distribution expectation of a sample estimator of the third central moment:

Applications  (21)

Converting Formal Moments  (2)

Convert raw moments to central moments:

Factorial moments:

Cumulants:

Show all cross-conversions between formal moments:

Show multivariate cross-conversions between formal moments:

Analysis of Estimators  (6)

Compute a sample estimator of the variance:

Compute the bias of the estimator as the mean with respect to the sampling population distribution, assuming a sample of size :

Illustrate the computation by evaluating the estimator on a symbolic sample of size 5:

Now compute its expectation assuming are independent random variates from normal distribution:

Compare with the result obtained above:

Compute the expected variance of a sample estimator of the variance:

Compute the variance as the second central moment of the estimator:

In the large sample size limit, the variance of the estimator tends to zero in agreement with the law of large numbers:

Perform 1000 simulations using standard normal samples of size 30:

Compare the sample mean and variance to their expected values:

Compute covariance between the sample mean and sample variance estimators:

Compute sampling population covariance as a mixed central moment:

The expected covariance vanishes on normal samples:

Find a sample estimator of the off-diagonal covariance matrix element of two-dimensional data:

Find its bias and its variance:

Compute the bias and the variance of the estimator for binormal samples:

Estimate the sample size needed for the variance of the estimator on standard binormal samples with not to exceed 0.001:

The sample estimator of the standard deviation is computed as the square root of the sample variance:

Such an estimator is biased and underestimates the population standard deviation:

The analysis of the standard deviation estimator is carried out by replacing the nonlinear function with its truncated Taylor series about the bias of its argument:

Find the expectation of the approximated estimator:

Compute its numerical value for a standard normal sample of size :

Find the variance of the estimator for normal samples:

Derive finite-sample Jarque–Bera statistics :

Find the mean and variance of sample skewness estimator on size normal samples:

Compute the mean and variance of sample kurtosis estimator on size normal samples:

Assemble the estimator:

Find large approximation:

Unbiased Raw Moment Estimators  (2)

Sample moment estimators are automatically unbiased:

Compute an unbiased moment estimator in terms of power symmetric polynomials:

Compute the sampling population expectation of the estimator:

Compute the multivariate moment estimator:

These are also unbiased:

Evaluate the estimator on a symbolic sample:

Unbiased Factorial Moment Estimators  (1)

Factorial moments can be expressed as the linear combination of raw moments:

Hence their sample estimators are automatically unbiased as well:

Compute an unbiased factorial moment estimator in terms of power symmetric polynomials:

Compute the sampling population expectation of the estimator:

Unbiased Central Moment Estimators  (3)

Find the second h-statistics:

Write the h-statistics in terms of power symmetric polynomials:

Compare it with the sample estimator of the second central moment :

Find the sampling population expectation of these estimators for sample size :

Compute the third h-statistics in terms of power symmetric polynomials:

Compare it with the sample estimator of central moment :

Find the sampling population expectation of these estimators for sample size :

Find multivariate h-statistics for :

Evaluate the estimator on a sample from a binormal distribution:

Compare with the population value:

Unbiased Cumulant Estimators  (2)

Find fourth k-statistics in terms of power symmetric polynomials:

Evaluate obtained k-statistics on a standard normal sample:

Accumulate statistics of the estimator and show the histogram:

Compute multivariate k-statistics for :

Compare it to the sample estimator:

Compound Estimators  (3)

Find the unbiased estimator of the second power of mean:

Evaluate it on a symbolic sample:

Find the sample population expectation:

Compute the unbiased estimator of the product of cumulants, also known as polykay:

Express it in terms of power symmetric polynomials:

Find the unbiased estimator of the product of multivariate central moments, also known as polyache:

Find the value of the estimator on a multivariate sample:

Compare with sampling population moments:

Cumulants of k-Statistics  (1)

Cumulants of k-statistics are polynomials in sampling population expectations of certain monomials of k-statistics. They are built using umbral calculus, starting with expression of the multivariate cumulant in terms of raw moments:

Each multivariate moment is understood as the sampling population expectation of the monomial in k-statistics. For instance, raw moment stands for the product of expectation of . Find the resulting unbiased estimator for and :

Define a procedure for computation of cumulants of k-statistics:

Verify that :

Verify that :

This implies that the sample mean and sample variance of a normal sample are independent:

Cumulants of k-statistics were tabulated because they were thought to give more concise expressions, and were used for computation of moments of estimators. Compute the cumulant of second k-statistics:

Compute the cumulant of the product of k-statistics:

Expressions for higher-order cumulants of k-statistics quickly become big:

Combinatorial Uses of MomentConvert  (1)

Compute the number of partitions of a set into subsets of given sizes:

There are 10 ways to partition the set of 5 elements into subsets of 2 and 3 elements:

Construct partitions and count directly:

Properties & Relations  (5)

The binomial theorem defines relations between formal moments and formal central moments:

Express formal factorial moments in terms of formal moments using Stirling numbers:

Polynomial in moments rewritten in terms of central moments may still involve the mean :

The sample estimator of factorial moment is unbiased:

Compute cumulants through series expansion of logarithm of moment-generating function:

Possible Issues  (2)

Conversion between forms of symmetric polynomials treats formal moments as constants:

Expressions involving AugmentedSymmetricPolynomial and PowerSymmetricPolynomial are converted:

MomentConvert requires input to be polynomial in formal and/or sample moments:

Neat Examples  (2)

Cross convert between any pairs of formal moments:

Cross convert between any pairs of multivariate formal moments:

Wolfram Research (2010), MomentConvert, Wolfram Language function, https://reference.wolfram.com/language/ref/MomentConvert.html.

Text

Wolfram Research (2010), MomentConvert, Wolfram Language function, https://reference.wolfram.com/language/ref/MomentConvert.html.

CMS

Wolfram Language. 2010. "MomentConvert." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MomentConvert.html.

APA

Wolfram Language. (2010). MomentConvert. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MomentConvert.html

BibTeX

@misc{reference.wolfram_2024_momentconvert, author="Wolfram Research", title="{MomentConvert}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/MomentConvert.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_momentconvert, organization={Wolfram Research}, title={MomentConvert}, year={2010}, url={https://reference.wolfram.com/language/ref/MomentConvert.html}, note=[Accessed: 21-December-2024 ]}