MomentEvaluate

MomentEvaluate[mexpr,dist]

evaluates formal moments in the moment expression mexpr on the distribution dist.

MomentEvaluate[mexpr,list]

evaluates formal moments and formal sample moments in mexpr on the data list.

MomentEvaluate[mexpr,dist,list]

evaluates formal moments on the distribution dist and formal sample moments on the data list.

Details

  • A moment expression is an expression involving formal moments and formal sample moments.
  • A formal moment is an expression of the form:
  • Moment[r]formal r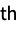^(th) moment
    CentralMoment[r]formal r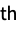^(th) central moment
    FactorialMoment[r]formal r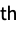^(th) factorial moment
    Cumulant[r]formal r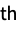^(th) cumulant
  • A formal sample moment is an expression of the form:
  • PowerSymmetricPolynomial[r]formal r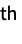^(th) power symmetric polynomial
    AugmentedSymmetricPolynomial[{r1,r2,…}]formal {r1,r2,…} augmented symmetric polynomial
  • For a sample moment expression PowerSymmetricPolynomial[0] is taken to be the length of the list of data.
  • MomentEvaluate[mexpr,…,n] assumes that n is taken to be the length of the list of data.

Examples

open allclose all

Basic Examples  (3)

Evaluate formal moments for a univariate distribution:

Evaluate formal moments for a multivariate distribution:

Evaluate sample formal moments for data:

Evaluate formal moments for data:

Scope  (6)

Evaluate mixed univariate formal moment polynomial for a distribution:

Evaluate mixed multivariate formal moment polynomial for a distribution:

Evaluate polynomial in formal moments for data:

Compare with direct evaluation:

Evaluate formal sample polynomial for data:

Evaluate formal sample polynomial for data with n being the sample size:

Evaluate an expression containing both formal moments and formal sample moments:

Alternatively:

Generalizations & Extensions  (1)

Compute mean, variance, skewness, and excess kurtosis expressed in terms of Cumulant:

Compare with direct evaluation:

Applications  (2)

Find expectation of estimator on a sample from Bernoulli distribution:

Express the expectation of the estimator in terms of formal moments:

Expectation of the estimator for a sample from Bernoulli distribution:

Variance of the sample estimator:

Construct sample and unbiased estimators for :

Accumulate statistics of these estimators on the same data:

Compare the means of these statistics with population cumulant:

Find sampling population expectation of estimators for distribution dist:

Find sampling population variance of estimators for distribution dist:

Numerically evaluate expected variances for sample sizes used:

Compare to sample values:

Properties & Relations  (1)

MomentEvaluate effectively evaluates a moment expression by evaluating its constituents:

Wolfram Research (2010), MomentEvaluate, Wolfram Language function, https://reference.wolfram.com/language/ref/MomentEvaluate.html.

Text

Wolfram Research (2010), MomentEvaluate, Wolfram Language function, https://reference.wolfram.com/language/ref/MomentEvaluate.html.

CMS

Wolfram Language. 2010. "MomentEvaluate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MomentEvaluate.html.

APA

Wolfram Language. (2010). MomentEvaluate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MomentEvaluate.html

BibTeX

@misc{reference.wolfram_2024_momentevaluate, author="Wolfram Research", title="{MomentEvaluate}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/MomentEvaluate.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_momentevaluate, organization={Wolfram Research}, title={MomentEvaluate}, year={2010}, url={https://reference.wolfram.com/language/ref/MomentEvaluate.html}, note=[Accessed: 21-December-2024 ]}