 |
Search for all pages containing StationaryWaveletTransform
BUILT-IN MATHEMATICA SYMBOL
StationaryWaveletTransform
StationaryWaveletTransform[data]
gives the stationary wavelet transform (SWT) of an array of data.
StationaryWaveletTransform[data, wave]
gives the stationary wavelet transform using the wavelet wave.
StationaryWaveletTransform[data, wave, r]
gives the stationary wavelet transform using r levels of refinement.
StationaryWaveletTransform[image, ...]
gives the stationary wavelet transform of an image.
StationaryWaveletTransform[sound, ...]
gives the stationary wavelet transform of sampled sound.
Details and Options
- StationaryWaveletTransform gives a DiscreteWaveletData object.
- Properties of the DiscreteWaveletData dwd can be found using dwd["prop"], and a list of available properties can be found using dwd["Properties"].
- StationaryWaveletTransform is similar to DiscreteWaveletTransform except that no subsampling occurs at any refinement level and the resulting coefficient arrays all have the same dimensions as the original data.
- The data can be a rectangular array of any depth.
- By default, input image is converted to an image of type
. - The resulting wavelet coefficients are arrays of the same depth and dimensions as the input data.
- The possible wavelets wave include:
-
BattleLemarieWavelet[...] Battle-Lemarié wavelets based on B-spline BiorthogonalSplineWavelet[...] B-spline-based wavelet CoifletWavelet[...] symmetric variant of Daubechies wavelets DaubechiesWavelet[...] the Daubechies wavelets HaarWavelet[...] classic Haar wavelet MeyerWavelet[...] wavelet defined in the frequency domain ReverseBiorthogonalSplineWavelet[...] B-spline-based wavelet (reverse dual and primal) ShannonWavelet[...] sinc function-based wavelet SymletWavelet[...] least asymmetric orthogonal wavelet - The default wave is HaarWavelet[].
- With higher settings for the refinement level r, larger-scale features are resolved.
- The default refinement level r is given by
![TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor]](Files/StationaryWaveletTransform.en/2.png "TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor]")
, where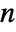 
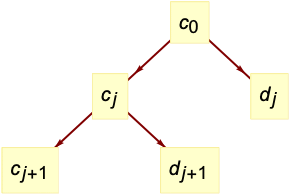
is the minimum dimension of data. » - The tree of wavelet coefficients at level
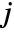consists of coarse coefficients 
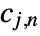and detail coefficients 
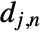, with 
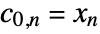representing the input data. -
- The forward transform is given by
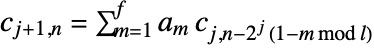and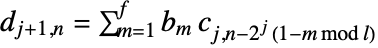 
, where 
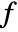is the filter length for the corresponding wspec and 
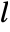is the length of input data. » - The inverse transform is given by
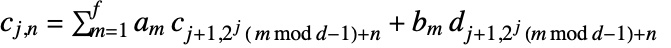. » - The
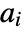are lowpass filter coefficients and 
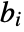are highpass filter coefficients that are defined for each wavelet family. - The dimensions of
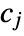and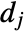 
are the same as input data dimensions. - The following options can be given:
-
Method Automatic method to use WorkingPrecision MachinePrecision precision to use in internal computations - StationaryWaveletTransform uses periodic padding of data.
- InverseWaveletTransform gives the inverse transform.
Examplesopen all
Basic Examples (3)
Compute a stationary wavelet transform using the HaarWavelet:
| In[1]:= |
| Out[1]= |  |
Use Normal to view all coefficients:
| In[2]:= |
| Out[2]= |  |
Transform an Image object:
| In[1]:= |
| Out[1]= |  |
Use 
to extract coefficient images:
| In[2]:= |
| Out[2]= |  |
Compute the inverse transform:
| In[3]:= |
| Out[3]= |  |
Transform a sampled Sound object:
| In[1]:= |
| Out[1]= |  |
| In[2]:= |
| Out[2]= |  |
| In[3]:= |
| Out[3]= |  |
New in 8
