StructuralImportance

StructuralImportance[rdist]

gives the structural importances for all components in the ReliabilityDistribution rdist.

StructuralImportance[fdist]

gives the structural importances for all components in the FailureDistribution fdist.

StructuralImportance[bexpr,{x1,x2,…}]

gives the structural importance for the components x1, x2, … in the Boolean expression bexpr.

Details

  • StructuralImportance is also known as Birnbaum's structural importance.
  • The structural importance for component 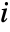is the fraction of the system states in which component 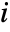is working, where a failure of component 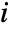will result in a failure of the system.
  • For StructuralImportance[fdist] and StructuralImportance[rdist], the results are returned in the component order given in the distribution list in rdist or fdist.
  • For StructuralImportance[bexpr,{x1,x2,…}], the results are returned in the order {x1,x2,…}.
  • StructuralImportance[bexpr,…] is defined when UnateQ[bexpr] is True.

Examples

open allclose all

Basic Examples  (4)

Two components connected in series:

The result is given in the same order as the distribution list in ReliabilityDistribution:

Two components connected in parallel:

Use the structure function directly, without lifetime distributions:

Use fault tree-based modeling to define the system:

Scope  (18)

Boolean Expression Models  (5)

Both components in a parallel structure have the same structural importance:

Structural importance for a serial structure:

Structural importance for components in a 2-out-of-3 network:

Importance for a mixed system:

Importance for a mixed system:

ReliabilityDistribution Models  (7)

Two components connected in parallel:

Both components are equally important:

Two components connected in series:

Importance is the same:

A system where two out of three components need to work:

Components are equally important:

A simple mixed system:

Component is more important:

A system with a series connection in parallel with a component:

The single component is more important:

One component in parallel with two others, with different distributions:

Find the importance measures at one specific point in time as exact results:

As machine-precision results:

Model the system in steps to get the importance measure for a subsystem:

FailureDistribution Models  (6)

Any of two basic events lead to the top event:

Both events have the same importance:

Only both basic events together lead to the top event:

Serial events are equally important:

A voting gate, with identical distributions on the basic events:

The events have the same structural importance:

A simple system with both And and Or gates:

The basic event is most important:

A simple system with both And and Or gates:

Compute the importance:

Model the system in steps to get importance measure for a subsystem:

Applications  (4)

Two points in a city are connected through a network of water pipes . Find the pipes most critical to maintain the supply of water:

Pipe is most important:

Analyze what component is most likely to have caused a failure at the launch of an aircraft. The hangar door can be opened electronically or manually:

Two fuel pumps require power to run:

Two more pumps run on reliable batteries, giving the following fuel transfer structure:

Also needed is deicing of the aircraft and a fuel storage tank:

Compute the importance:

Deicing and fuel storage have the highest structural importance:

StructuralImportance is also called the Banzhaf power index and measures the probability of changing the outcome of a voting procedure. Consider a county board with the following districts and votes:

Find all combinations of district votes that will give a majority:

The Boolean expression for a decision achieving a majority:

None of the Oyster Bay, Glen Cove, and Long Beach districts can change the outcome of a vote alone:

Compute the Banzhaf power index of the states in the 1804 US presidential election:

Compare with the population in the respective states:

Population on the inner pie, power index on the ring:

As a plot of population and power index:

Compare the power index with the dates they joined the union:

Properties & Relations  (4)

Structural importance is independent of the lifetime distributions:

The result does not contain any of the distribution parameters:

It is equivalent to the specification without the distributions:

Structural importance is BirnbaumImportance where components have probability :

Irrelevant components do not influence the importance of other components:

Irrelevant components have importance 0:

Structural importance for bexpr in ReliabilityDistribution is equal to bexpr in FailureDistribution:

Neat Examples  (1)

Show all the importance measures for a regular system structure:

Wolfram Research (2012), StructuralImportance, Wolfram Language function, https://reference.wolfram.com/language/ref/StructuralImportance.html.

Text

Wolfram Research (2012), StructuralImportance, Wolfram Language function, https://reference.wolfram.com/language/ref/StructuralImportance.html.

CMS

Wolfram Language. 2012. "StructuralImportance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StructuralImportance.html.

APA

Wolfram Language. (2012). StructuralImportance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StructuralImportance.html

BibTeX

@misc{reference.wolfram_2024_structuralimportance, author="Wolfram Research", title="{StructuralImportance}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/StructuralImportance.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_structuralimportance, organization={Wolfram Research}, title={StructuralImportance}, year={2012}, url={https://reference.wolfram.com/language/ref/StructuralImportance.html}, note=[Accessed: 21-November-2024 ]}