 |
BUILT-IN MATHEMATICA SYMBOL
SymmetricPolynomial
SymmetricPolynomial[k, {x1, ..., xn}]
gives the k
elementary symmetric polynomial in the variables 
.
Details
- A symmetric polynomial of n variables
is invariant under any permutation of its variables. The k
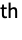elementary symmetric polynomial is the sum of all square-free monomials of degree k. - The degree k must satisfy
. - The elementary symmetric polynomials form a basis for the symmetric polynomials.
- Expressing a general symmetric polynomial in terms of elementary symmetric polynomials is accomplished by using SymmetricReduction.
Examplesopen all
Basic Examples (1)
The elementary symmetric polynomial of degree 3 in variables 
:
| In[1]:= |
| Out[1]= |  |
New in 6
