Ordinary Differential Equations (ODEs)
| Overview of ODEs | Higher-Order ODEs |
| First Order ODEs | Systems of ODEs |
| Linear Second-Order ODEs | Nonlinear ODEs with Lie Symmetries |
| Nonlinear Second-Order ODEs | Fractional Differential Equations |
Overview of ODEs
There are four major areas in the study of ordinary differential equations that are of interest in pure and applied science.
- Exact solutions, which are closed-form or implicit analytical expressions that satisfy the given problem.
- Numerical solutions, which are available for a wider class of problems, but are typically only valid over a limited range of the independent variables.
- Qualitative theory, which is concerned with the global properties of solutions and is particularly important in the modern approach to dynamical systems.
- Existence and uniqueness theorems, which guarantee that there are solutions with certain desirable properties provided a set of conditions is fulfilled by the differential equation.
Of these four areas, the study of exact solutions has the longest history, dating back to the period just after the discovery of calculus by Sir Isaac Newton and Gottfried Wilhelm von Leibniz. The following table introduces the types of equations that can be solved by DSolve.
name of equation | general form | date of discovery | mathematician |
| separable | 1691 | G. Leibniz | |
| homogeneous | 1691 | G. Leibniz | |
| linear first-order ODE | 1694 | G. Leibniz | |
| Bernoulli | 1695 | James Bernoulli | |
| Riccati | 1724 | Count Riccati | |
| exact first-order ODE | 1734 | L. Euler | |
| Clairaut | 1734 | A-C. Clairaut | |
| linear with constant coefficients | 1743 | L. Euler | |
| hypergeometric | 1769 | L. Euler | |
| Legendre | 1785 | M. Legendre | |
| Bessel | 1824 | F. Bessel | |
| Mathieu | 1868 | E. Mathieu | |
| Abel | 1834 | N. H. Abel | |
| Chini | 1924 | M. Chini |
Examples of ODEs belonging to each of these types are given in other tutorials (clicking a link in the table will bring up the relevant examples).
First Order ODEs
Straight Integration
Separable Equations
Even when variables can be separated, the final solution might be accompanied by a warning message from Solve, or it might only be given as an InverseFunction object.
Homogeneous Equations
Linear First-Order Equations
Inverse Linear Equations
It may happen that a given ODE is not linear in ![]() but can be viewed as a linear ODE in
but can be viewed as a linear ODE in ![]() . In this case, it is said to be an inverse linear ODE.
. In this case, it is said to be an inverse linear ODE.
Bernoulli Equations
A Bernoulli equation is a first-order equation of the form
The problem of solving equations of this type was posed by James Bernoulli in 1695. A year later, in 1696, G. Leibniz showed that it can be reduced to a linear equation by a change of variable.
In general, the solution to a Bernoulli equation will consist of ![]() branches, where
branches, where ![]() is the degree of
is the degree of ![]() in the equation.
in the equation.
Riccati Equations
A Riccati equation is a first-order equation of the form
This equation was used by Count Riccati of Venice (1676–1754) to help in solving second-order ordinary differential equations.
Solving Riccati equations is considerably more difficult than solving linear ODEs.
Any Riccati equation can be transformed to a second-order linear ODE. If the latter can be solved explicitly, then a solution for the Riccati equation can be derived.
Exact Equations
If an equation is not exact, it may be possible to find an integrating factor (a multiplier for the functions P and Q, defined previously) that converts the equation into exact form. DSolve tries a variety of techniques to automatically find integrating factors in such situations.
Clairaut Equations
A Clairaut equation is a first-order equation of the form
A remarkable feature of this nonlinear equation is that its general solution has a very simple form.
The general solution to Clairaut equations is simply a family of straight lines.
Abel Equations
An Abel ODE is a first-order equation of the form
This equation arose in the context of the studies of Niels Henrik Abel on the theory of elliptic functions, and represents a natural generalization of the Riccati equation.
Associated with any Abel ODE is a sequence of expressions that is built from the coefficients of the equation ![]() and invariant under certain coordinate transformations of the independent variable and the dependent variable. These invariants characterize each equation and can be used for identifying integrable classes of Abel ODEs. In particular, Abel ODEs with zero or constant invariants can be integrated easily and constitute an important integrable class of these equations.
and invariant under certain coordinate transformations of the independent variable and the dependent variable. These invariants characterize each equation and can be used for identifying integrable classes of Abel ODEs. In particular, Abel ODEs with zero or constant invariants can be integrated easily and constitute an important integrable class of these equations.
Another important class of integrable Abel ODEs are those that can be reduced to inverse linear first-order ODEs using a nonlinear coordinate transformation.
Another important class of integrable Abel ODEs consists of those that can be transformed to an inverse Riccati equation. Since Riccati equations can be transformed to second-order linear ODEs, the solutions for this class are usually given in terms of special functions such as AiryAi and BesselJ.
The Abel ODEs considered so far are said to be of the first kind. Abel ODEs of the second kind are given by the following general formula.
An Abel ODE of the second kind can be converted to an equation of the first kind with a coordinate transformation. Thus, the solution methods for this kind of Abel ODE are identical to the methods for equations of the first kind.
Chini Equations
Chini equations are a generalization of Abel and Riccati equations.
Singular Solutions
By default, DSolve returns a general solution depending on arbitrary parameters for a linear or nonlinear ODE. For some nonlinear ODEs such as the Clairaut equation or the logistic equation, there can also be singular solutions. These singular solutions cannot be obtained by assigning specific values to the arbitrary constants in the general solution, but are useful in the study of dynamical systems and elsewhere.
The DSolve option IncludeSingularSolutionsTrue returns singular solutions for nonlinear ODEs together with the general solution.
Linear Second-Order ODEs
Overview
Solving linear first-order ODEs is straightforward and only requires the use of a suitable integrating factor. In sharp contrast, there are a large number of methods available for handling linear second-order ODEs, but the solution to the general equation belonging to this class is still not available. Therefore the linear case is discussed in detail before moving on to nonlinear second-order ODEs.
The general linear second-order ODE has the form
Here, ![]() ,
, ![]() , and
, and ![]() are arbitrary functions of
are arbitrary functions of ![]() . The term "linear" refers to the fact that the degree of each term in
. The term "linear" refers to the fact that the degree of each term in ![]() ,
, ![]() and
and ![]() is 1. (Thus, terms like
is 1. (Thus, terms like ![]() or
or ![]() would make the equation nonlinear.)
would make the equation nonlinear.)
Equations with Constant Coefficients
The simplest type of linear second-order ODE is one with constant coefficients.
Notice that the general solution is a linear combination of two exponential functions. The arbitrary constants C[1] and C[2] can be varied to produce particular solutions.
The exponents ![]() and
and ![]() in the basis
in the basis ![]() are obtained by solving the associated quadratic equation. This quadratic equation is called the auxiliary or characteristic equation.
are obtained by solving the associated quadratic equation. This quadratic equation is called the auxiliary or characteristic equation.
The roots are real and distinct in this case. There are two other cases of interest: real and equal roots, and imaginary roots.
Euler and Legendre Equations
An Euler equation has the general form
Euler equations can be solved by transforming them to equations with constant coefficients.
The Legendre linear equation is a generalization of the Euler equation. It is an ODE of the form
Exact Equations
A linear second-order ordinary differential equation
An exact linear second-order ODE is solved by reduction to a linear first-order ODE.
Equations with Solutions Involving Special Functions
DSolve can find solutions for most of the standard linear second-order ODEs that occur in applied mathematics.
These special functions can be expressed in terms of elementary functions for certain values of their parameters. The Wolfram Language performs this conversion automatically wherever it is possible.
As a result of these conversions, the solutions of certain ODEs can be partially expressed in terms of elementary functions. Hermite's equation is one such ODE.
The solutions of next few ODEs are expressed in terms of Heun functions.
Equations with Rational Coefficients
The hypergeometric functions play a unifying role in mathematical analysis since many important functions, such as the Bessel functions and Legendre functions, are special cases of them. Each hypergeometric function is associated with a linear ODE having rational coefficients.
DSolve can solve a large class of second-order linear ODEs by reducing them to the ODEs for hypergeometric functions. The reduction involves coordinate transformations of both the independent and dependent variables.
The ODEs for special functions have been studied since the eighteenth century. During the last 30 years, powerful algorithms have been developed for systematically solving ODEs with rational coefficients. An important algorithm of this type is Kovacic’s algorithm, a decision procedure that either generates a solution for the given ODE in terms of Liouvillian functions or proves that the given ODE does not have a Liouvillian solution.
The solution returned from Kovacic's algorithm may occasionally include functions such as ExpIntegralEi or an unevaluated integral of elementary functions because, while it is easy to find a second solution for a second-order linear ODE once one solution is known, the integral involved in finding the second solution may be hard to evaluate explicitly.
In general, the solutions for linear ODEs with rational coefficients and order greater than one can be given in terms of DifferentialRoot objects. This is similar to the representation for solutions of polynomial equations in terms of Root.
Equations with Non-Rational Coefficients
The ODEs that arise in practical applications often have non-rational coefficients. In such cases, DSolve attempts to convert the equation into one with rational coefficients using a suitable coordinate transformation.
Inhomogeneous Equations
If the given second-order ODE is inhomogeneous, DSolve applies either the method of variation of parameters or the method of undetermined coefficients to return a solution for the problem.
The method of undetermined coefficients is used for solving inhomogeneous linear ODEs with constant coefficients, if the inhomogeneous term has the form ![]() and its subforms, where
and its subforms, where ![]() and
and ![]() are polynomial functions of
are polynomial functions of ![]() .
.
Nonlinear Second-Order ODEs
The general form of a nonlinear second-order ODE is
For simplicity, assume that the equation can be solved for the highest-order derivative ![]() to give
to give
There are a few classes of nonlinear second-order ODEs for which solutions can be easily found.
The first class consists of equations that do not explicitly depend on ![]() ; that is, equations of the form
; that is, equations of the form ![]() . Such equations can be regarded as first-order ODEs in
. Such equations can be regarded as first-order ODEs in ![]() .
.
As in the case of linear second-order ODEs, the solution depends on two arbitrary parameters C[1] and C[2].
The second class of easily solvable nonlinear second-order equations consists of equations that do not depend explicitly on ![]() or
or ![]() ; that is, equations of the form
; that is, equations of the form ![]() . These equations can be reduced to first-order ODEs with independent variable
. These equations can be reduced to first-order ODEs with independent variable ![]() . Inverse functions are needed to give the final solution for
. Inverse functions are needed to give the final solution for ![]() .
.
The third class consists of equations that do not depend explicitly on ![]() ; that is, equations of the form
; that is, equations of the form ![]() . Once again, these equations can be reduced to first-order ODEs with independent variable
. Once again, these equations can be reduced to first-order ODEs with independent variable ![]() .
.
The fourth class consists of equations that are homogeneous in some or all of the variables ![]() ,
, ![]() , and
, and ![]() . There are several possibilities in this case, but here only the following simple example is considered.
. There are several possibilities in this case, but here only the following simple example is considered.
The fifth and final class of easily solvable nonlinear second-order ODEs consists of equations that are exact or can be made to be exact using an integrating factor.
It is important to note that the solutions to fairly simple-looking nonlinear ODEs can be complicated. Verifying and applying the solutions in such cases is a difficult problem.
Higher-Order ODEs
Overview
The general form of an ODE with order ![]() is
is
As in the case of second-order ODEs, such an ODE can be classified as linear or nonlinear. The general form of a linear ODE of order ![]() is
is
If ![]() is the zero function, the equation is said to be homogeneous. This discussion is primarily restricted to that case.
is the zero function, the equation is said to be homogeneous. This discussion is primarily restricted to that case.
Many methods for solving linear second-order ODEs can be generalized to linear ODEs of order ![]() , where
, where ![]() is greater than 2. If the order of the ODE is not important, it is simply called a linear ODE.
is greater than 2. If the order of the ODE is not important, it is simply called a linear ODE.
Equations with Constant Coefficients
A linear ODE with constant coefficients can be easily solved once the roots of the auxiliary equation (or characteristic equation) are known. Some examples of this type follow.
Higher-Order Euler and Legendre Equations
An Euler equation is an ODE of the form
The Legendre linear equation is a generalization of the Euler equation. It has the form
Exact Higher-Order Equations
A linear ordinary differential equation of order ![]()
The condition of exactness can be used to reduce the problem to that of solving an equation of order ![]() .
.
Further Examples of Higher-Order Equations
The solutions to many second-order ODEs can be expressed in terms of special functions. Solutions to certain higher-order ODEs can also be expressed using AiryAi, BesselJ, and other special functions.
As for second-order linear ODEs, there are modern algorithms for solving higher-order ODEs with rational coefficients. These algorithms give "rational-exponential" solutions, which are combinations of rational functions and exponentials of the integrals of rational functions. These algorithms are combined with techniques such as reduction of order to produce a complete solution for the given ODE.
The equations considered so far have been homogeneous; that is, with no term free of ![]() or its derivatives. If the given ODE is inhomogeneous, DSolve applies either the method of variation of parameters or the method of undetermined coefficients to obtain the solution.
or its derivatives. If the given ODE is inhomogeneous, DSolve applies either the method of variation of parameters or the method of undetermined coefficients to obtain the solution.
Thus, the general solution for the inhomogeneous equation is the sum of the general solution to the homogeneous equation and a particular integral of the ODE.
The solution methods for nonlinear ODEs of higher order rely to a great extent on reducing the problem to one of lower order.
Systems of ODEs
Overview
Systems of ODEs are important in various fields of science, such as the study of electricity and population biology. Like single ODEs, systems of ODEs can classified as linear or nonlinear.
A system of linear first-order ODEs can be represented in the form
Here ![]() is a vector of unknown functions,
is a vector of unknown functions, ![]() is the matrix of the coefficients of the unknown functions, and
is the matrix of the coefficients of the unknown functions, and ![]() is a vector representing the inhomogeneous part of the system.
is a vector representing the inhomogeneous part of the system.
In the two-dimensional case, the system can be written more concretely as
If all the entries of the matrix ![]() are constants, then the system is said to be linear with constant coefficients. If
are constants, then the system is said to be linear with constant coefficients. If ![]() is the zero vector, then the system is said to be homogeneous.
is the zero vector, then the system is said to be homogeneous.
The important global features of the solutions to linear systems can be clarified by considering homogeneous systems of ODEs with constant coefficients.
Linear Systems of ODEs
Linear systems of ODEs can also be solved in matrix form using vector variables and matrix variables.
Solving homogeneous systems of ODEs with constant coefficients and of arbitrary order is a straightforward matter. They are solved by converting them to a system of first-order ODEs.
In general, systems of linear ODEs with non-constant coefficients can only be solved in cases where the coefficient matrix has a simple structure, as illustrated in the following examples.
As for single ODEs, there are sophisticated modern algorithms for solving systems of ODEs with rational coefficients.
The systems considered so far have all been homogeneous. If the system is inhomogeneous (that is, if there are terms free from any dependent variables and their derivatives), DSolve applies either the method of variation of parameters or the method of undetermined coefficients to find the general solution.
Particular solutions to the system can be obtained by assigning values to the constants C[1] and C[2].
Nonlinear Systems of ODEs
Following are two examples of nonlinear systems of ODEs that can be solved symbolically using DSolve.
The previous two examples demonstrate that the solutions to fairly simple systems are usually complicated expressions of the independent variable. In fact, the solution is often available only in implicit form and may thus contain InverseFunction objects or unevaluated Solve objects.
Nonlinear ODEs with Lie Symmetries
Around 1870, Marius Sophus Lie realized that many of the methods for solving differential equations could be unified using group theory. Lie symmetry methods are central to the modern approach for studying nonlinear ODEs. They use the notion of symmetry to generate solutions in a systematic manner. Here is a brief introduction to Lie’s approach that provides some examples that are solved in this way by DSolve.
A key notion in Lie's method is that of an infinitesimal generator for a symmetry group. This concept is illustrated in the following example.
For a fixed value of ![]() , the point
, the point ![]() (in blue) can be obtained by rotating the line joining
(in blue) can be obtained by rotating the line joining ![]() (in red) to the origin through an angle of
(in red) to the origin through an angle of ![]() in the counterclockwise direction.
in the counterclockwise direction.
A rotation through ![]() can be represented by the matrix
can be represented by the matrix
The Lie symmetry method requires calculating a first-order approximation to the expressions for the group. This approximation is called an infinitesimal generator.
The rotation group arises in the study of symmetries of geometrical objects; it is an example of a symmetry group. The infinitesimal generator, a differential operator, is a convenient local representation for this symmetric group, which is a set of matrices.
An expression that reduces to 0 under the action of the infinitesimal generator is called an invariant of the group.
In the following examples, these ideas are applied to differential equations.
Now, the Riccati equation depends on three variables: ![]() ,
, ![]() , and
, and ![]() . Hence, the infinitesimal generator
. Hence, the infinitesimal generator ![]() must be prolonged to act on all three variables in this first-order equation.
must be prolonged to act on all three variables in this first-order equation.
Depending on the order of the given equation, the knowledge of a symmetry (in the form of an infinitesimal generator) can be used in three ways.
- If the order of the equation is 1, it gives an integrating factor for the ODE that makes the equation exact and hence solvable.
- It gives a set of canonical coordinates in which the equation has a simple (integrable) form.
- It reduces the problem of solving an ODE of order
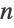 to that of solving an ODE of order
to that of solving an ODE of order  , which is typically a simpler problem.
, which is typically a simpler problem.
The DSolve function checks for certain standard types of symmetries in the given ODE and uses them to return a solution. Following are three examples of ODEs for which DSolve uses such a symmetry method.
Fractional Differential Equations
Fractional differential equations (FDEs) are differential equations involving fractional derivatives ![]() . These are generalizations of the ordinary differential equations that have attracted much attention and have been widely used in engineering, physics, chemistry, biology and other fields.
. These are generalizations of the ordinary differential equations that have attracted much attention and have been widely used in engineering, physics, chemistry, biology and other fields.
DSolve can solve any linear FDE with constant coefficients containing Caputo derivatives CaputoD.
The solution is given in terms of the MittagLefflerE function, which is the basic function for fractional calculus applications. Its role in the solutions of FDEs is similar to the role and importance of the Exp function for the solutions of ODEs: any FDE with constant coefficients can be solved in terms of Mittag–Leffler functions.
For Caputo-type FDEs, the initial conditions can always be given for integer order derivatives of dependent variable. The number of initial conditions depends on order ![]() of the FDE and is equal to
of the FDE and is equal to ![]() .
.
DSolve can also solve some linear systems of FDEs with constant coefficients. All equations in the system must have the same order ![]() .
.
This concludes the discussion of ordinary differential equations.