Defining Your Own Wavelet
You can define wavelets to plug into the wavelet analysis framework by using the correct template. A wavelet wave is of the form 
, where wfam is the symbol that indicates the wavelet family and args provide any necessary specification.
In order to set wfam as a wavelet family recognized by the system, the property 
must be set to True, where patt is a pattern that matches acceptable arguments args.
| WaveletQ | set to True if the symbol is a user wavelet |
Wavelet initialization property.
Both orthogonal and biorthogonal user wavelets are supported. Orthogonal wavelets are indicated by setting the property 
and, correspondingly, biorthogonal wavelets are set using the property 
.
| "OrthogonalQ" | set to True if the wavelet is orthogonal |
| "BiorthogonalQ" | set to True if the wavelet is biorthogonal |
Wavelet properties.
To compute primal lowpass filter coefficients, the property 
must be set; here prec indicates the precision of filter coefficients. Similarly, to compute dual lowpass filter coefficients, the property 
must be set. Both properties 
and 
are expected to return a list of the form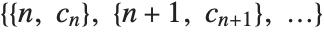 
, where 
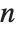is the index and 
is the corresponding filter coefficient. If a list of the form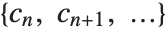 
is returned, it is assumed that index 
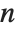starts from 0. An error message is generated if the filter coefficients 
are not numeric and indices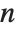 
are not integers.
Examples
Franklin Wavelet
Define a family of Franklin wavelets.
Franklin wavelet coefficients are given by the integral.
The above definition of a user wavelet can now be used to perform various wavelet operations.
Compute the filter coefficients.
| Out[10]= |  |
The scaling function is computed using the recursive equation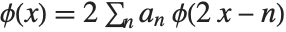 
, where 
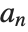represents the lowpass filter coefficients.
Compute the scaling function.
| Out[11]= |  |
Perform a wavelet transform.
| Out[12]= |  |
| Out[13]= |  |
Legendre Wavelet
Following is an example of the Legendre wavelet.
Although Legendre wavelets are not orthogonal, to be able to perform a wavelet transform, you need to set it to
True.
Specify the function to compute lowpass filter coefficients.
Compute the filter coefficients.
| Out[12]= |  |
| Out[13]= |  |
Compute the scaling function.
| Out[15]= |  |
The wavelet function is computed using the recursive equation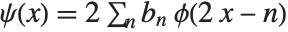 
, where 
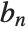represents the highpass filter coefficients.
Compute the wavelet function.
| Out[17]= |  |
Perform a wavelet transform.
| Out[153]= |  |
| Out[154]= |  |
Le Gall Wavelet
Generate a Le Gall wavelet.
Define
and
properties.
Use the Le Gall wavelet for thresholding.
| Out[7]= |  |
| Out[8]= |  |
| Out[9]= |  |
