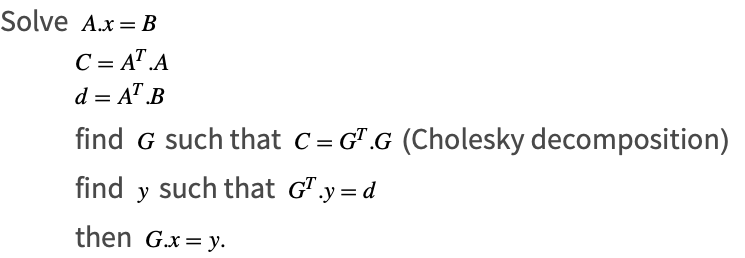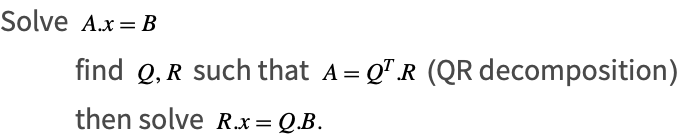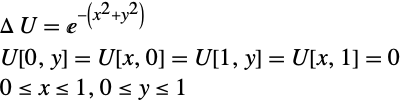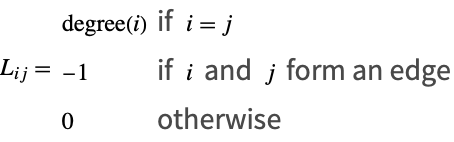OBSOLETE MATHEMATICA TUTORIAL
Additional functionality related to this tutorial has been introduced in subsequent versions of
Mathematica. For the latest information, see
Matrices and Linear Algebra.
Linear Algebra Examples
This tutorial shows a number of examples of the use of Mathematica for computations that involve linear algebra.
Matrix Ordering
Certain sparse matrix techniques try to reorder the matrix so that elements are grouped into blocks. The computation then works on each block using dense matrix techniques. One simple way to order a matrix into blocks involves sorting according to the sum of elements on each row. This will be demonstrated in this example.
First, generate a symmetric random sparse matrix.
Here is a plot of the matrix.
| Out[6]= |  |
Now compute a permutation of the matrix and then apply it to the matrix. This topic is discussed in "
Matrix Permutations".
Here is a plot of the reordered matrix; the effect of the reordering can be seen.
| Out[9]= |  |
Here is a much larger matrix with no structure and many random elements.
This is a plot of the original matrix.
| Out[17]= |  |
This plot of the reordered matrix shows that there are many rows and columns with no elements.
| Out[18]= |  |
Full Rank Least Squares Solutions
Solving a matrix equation 
is one of the key problems of matrix computation; techniques for solving it are discussed under "Solving Linear Systems". If 
is an 
×
matrix, this is a set of 
linear equations in 
unknowns. If 
, there are more equations than unknowns and the system is overdetermined. A general technique for finding least squares solutions is given under "Least Squares Solutions". This example will show some different techniques for finding approximate solutions to overdetermined systems for full rank matrices.
Note that all the example solutions in this section would work just as well if they were given sparse matrices as input.
Least Squares Cholesky
This technique uses a Cholesky decomposition to find a least squares solution. If a matrix 
has full rank, the solution can be found in the following way.
These steps can be placed into a
Mathematica function as follows.
The function can be applied as follows.
| Out[4]= |  |
The solution is close to satisfying the equation.
| Out[5]= |  |
| Out[6]= |  |
This technique is fast, but is less accurate because it computes 
.
This computes 1-, 2-, and
-norms for the solution that was found.
| Out[7]= |  |
Least Squares QR
When 
is full rank, a more accurate way to solve the problem is to use the QR decomposition as follows.
A
Mathematica program to find the solution is as follows.
The solution for this problem is very similar to the Cholesky solution.
| Out[4]= |  |
The QR decomposition solution can be more expensive than the Cholesky approach, but it is more accurate. An example that demonstrates the difference in accuracy is shown.
This shows how close the Cholesky solution is when using the 2-norm.
| Out[9]= |  |
This shows how close the QR solution is when using the 2-norm. It can be seen that the QR solution is a better approximation.
| Out[10]= |  |
Minimization of 1 and Infinity Norms
Many techniques for finding approximate solutions for the matrix equation 
when it is overdetermined (i.e., when 
) work by minimizing the 2-norm. This is because of certain advantages that make it computationally tractable. One reason is that the function
is differentiable and differentiation is a linear operation. Thus, a linear system can be formed that finds the minimizing solutions. Another reason is that the 2-norm is preserved under orthogonal transformations. This means that a range of equivalent problems can be formed, which may be easier to solve.
However, there are other solutions that can be found by minimizing other norms, such as the 1-norm or the 
-norm. These may be more desirable in the particular context because they may find solutions that maintain important properties relevant to the individual problem. In this example techniques are shown to find approximate solutions that minimize these norms; both will use a method to find minimum values of constrained linear problems; typically this is known as linear programming.
In Mathematica, linear programming is provided by the function LinearProgramming. This can solve the linear programming problem for the different types of numbers that Mathematica supports: integers and rational numbers, as well as machine-precision approximate real and arbitrary-precision approximate real numbers. In addition, it provides techniques that are suitable for minimizing extremely large systems by means of an interior point method.
The solutions given in this section are suitable for dense matrix input. It would be straightforward to modify them for sparse matrix input; this would be necessary to take full advantage of the interior point linear programming technique.
Note that the techniques in this section could be extended to add other constraints on the solution.
One-Norm Minimization
Minimizing the 1-norm involves finding the value of 
that minimizes the following.
This is done by forming new variables 
and finding the minimum.
This is implemented with the following program.
| Out[4]= |  |
Here 1-, 2-, and
-norms are computed for the solution that was found.
| Out[5]= |  |
Infinity-Norm Minimization
Minimizing the 
-norm is similar to minimizing the 1-norm. It involves finding the value of 
that minimizes the following.
This is done by forming new variables 
and finding the minimum.
This is implemented with the following program.
| Out[4]= |  |
Here 1-, 2-, and
-norms are computed for the solution that was found.
| Out[5]= |  |
Finite Difference Solutions
One way to solve partial differential equations is to form a spatial discretization and solve them with finite differences. This example considers a basic finite difference solution for the Poisson equation on a unit square.
This sets up the problem for an 80×80 grid with
. An abbreviated form of the variable matrix is printed out.
Out[3]//Short= |
| |  |
This is the finite difference formula for the differential operator.
In this step the application of the finite difference formula to the variable matrix is made. The boundary conditions are incorporated by allowing an overhang of one variable with a coefficient of zero around the boundary.
Here equations for the solutions on the grid are formed.
Out[6]//Short= |
| |  |
The approximate solution to the Poisson equation will be found by solving these equations. One way to solve the equations is to use
Solve, which will recognize the equations as linear and sparse and accordingly use a sparse matrix solver. Another method that also gives you the possibility of solving additional Poisson problems is to construct a matrix from the equations. The matrix represents the linear operator when the grid is flattened into a vector.
| Out[7]= |  |
| Out[8]= |  |
This repartitions the solution to restore the original structure.
This makes a contour plot of the solution.
| Out[10]= |  |
If you wanted to solve several Poisson equations with the same geometries but different right-hand functions, you could compute a factorization of the matrix and use it repeatedly. The way that
Mathematica allows you to repeat the factorization is described under "
Saving the Factorization".
| Out[11]= |  |
Now you just need to give it a vector representing the function
Cos[6x2+3y2] on the grid.
This passes the vector to the factorization, thereby finding the solution.
| Out[14]= |  |
It should be noted that this solution is only available at discrete points in the interior of the region. It does not include the value on the boundary or at other points in the interior. If the solution was to be used for other computational purposes this might be a limitation.
PadLeft and
PadRight could be used to add the boundary value and
Interpolation used to generate an interpolating function for the region.
| Out[17]= |  |
This uses
Plot3D to plot the solution.
| Out[18]= |  |
Now the solution can be computed at any position in the region.
| Out[19]= |  |
Mesh Partitioning
This example demonstrates a practical use for extreme eigenvalues. The aim is to partition the vertices of a mesh/graph into two subdomains, with each part having roughly equal numbers of vertices and with the partition cutting through as few edges as possible. (An edge is cut if its two vertices lie in each of the two subdomains.) One way to partition a graph is to form the Laplacian and use its Fiedler vector (the eigenvector that corresponds to the second smallest eigenvalue) to order the vertices. There are more efficient algorithms for graph partitioning that do not require the calculation of the eigenvector, but the approach using Fiedler remains an important one.
Data
This is the data for the coordinates of the vertices.
This is a list of triangles that forms the mesh.
Plotting the Mesh
To plot the mesh, simply plot each of the triangles.
| Out[8]= |  |
The Laplacian
A Laplacian of a graph, 
, is an 
×
sparse matrix, with 
the number of vertices in the graph. The entries of 
are mostly zero, except that the diagonals are positive integers that correspond to the degree of the vertex, where the degree is the number of vertices linked to the vertex. In addition, if two vertices, 
and 
, are joined by an edge, the entry 
is -1.
For the mesh here, the off-diagonals are given by the sparse array
.
| Out[10]= |  |
Each diagonal in a row is the negated sum of the off-diagonals. Thus the diagonal part of matrix is as follows.
| Out[11]= |  |
Therefore, the Laplacian is given as shown here.
| Out[12]= |  |
This visualizes the matrix.
| Out[13]= |  |
The Fiedler Vector
The sum of each row is zero, therefore the Laplacian matrix is positive semi-definite with a zero eigenvalue. The eigenvector corresponding to the second smallest eigenvalue is called the Fiedler vector.
This calculates the two smallest eigenvalues and eigenvectors.
One of these eigenvalues is zero.
| Out[15]= |  |
Partitioning the Nodes
Now use the Fiedler eigenvector to generate an ordering of vertices and form two groups of vertices:
and
.
This sets the colors of vertices in
as
Hue[0.] (red) and vertices in
as
Hue[0.75] (blue).
This plots the partition. As can be seen, the partitions avoided the very dense part of the mesh, and each subdomain is nicely connected.
| Out[23]= |  |
The number of edges cut by the partition can be calculated as follows.
| Out[26]= |  |
Matrix Functions with NDSolve
One of the important features of many of Mathematica's numerical solvers is that they work for vector and matrix input. Typically this is used to solve coupled systems of equations, but it can be used to solve matrix specific problems. One example will be given here that uses the numerical differential equation solver, NDSolve, to find parametrized solutions to matrix functions.
Out[2]//MatrixForm= |
| |  |
The exponential function is the solution of the differential equation.
This can be demonstrated by solving the equation symbolically.
| Out[3]= |  |
The matrix exponential
Exp[A t] can be found by forming a matrix equation and solving with
NDSolve. The solution here is valid for
.
| Out[5]= |  |
The solution is a function that will return the matrix function
Exp[A t] for a range of
t. If
t is 0.0, the identity matrix is returned.
Out[6]//MatrixForm= |
| |  |
This demonstrates that
Exp[A].Exp[A ]=Exp[2A].
Out[8]//MatrixForm= |
| |  |
Mathematica already has a function for computing the exponential of a function,
MatrixExp. This can be compared with the solution that was computed.
| Out[10]= |  |
Here is a differential equation for the
Sin function.
| Out[11]= |  |
This computes the
Sin of the matrix
A.
| Out[13]= |  |
The
Sin of the matrix has the correct behavior at the origin.
Out[14]//MatrixForm= |
| |  |
This computes the
Cos of the matrix
A.
| Out[16]= |  |
The
Cos of the matrix has the correct behavior at the origin.
Out[17]//MatrixForm= |
| |  |
This demonstrates the identity
, for
.
Out[18]//MatrixForm= |
| |  |
