15.3 Definite Integrals
Definite integration.
Here is the integral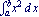 
.
In[1]:= Integrate[x^2, {x, a, b}]
Out[1]=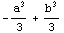 
Either of the limits of integration can be infinite.
In[2]:= Integrate[2 E ^ x Sin[x], {x, -Infinity, t}]
Out[2]=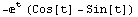 
This gives the multiple integral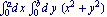 
.
In[3]:= Integrate[x^2 + y^2, {x, 0, a}, {y, 0, b}]
Out[3]=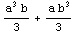 
The y integral is done first. Its limits can depend on the value of x. This ordering is the same as is used in functions like Sum and Table.
In[4]:= Integrate[x^2 + y^2, {x, 0, a}, {y, 0, x}]
Out[4]=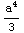 
You can often do a definite integral by first finding the indefinite one and then explicitly substituting in the limits. You have to be careful, however, when the integration region contains a singularity. The integral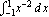 
, for example, has an indefinite form that is finite at each end point. Nevertheless, the integrand has a double pole at 
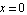, and the true integral is infinite.
