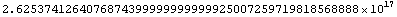
2.4 Arbitrary-Precision Calculations
When you use N to get a numerical result, Mathematica TE does what a standard calculator would do: it gives you a result to a fixed number of significant figures. You can also tell Mathematica TE exactly how many significant figures to keep in a particular calculation. This allows you to get numerical results in Mathematica TE to any degree of precision.
Numerical evaluation functions.
This gives the numerical value of 
to a fixed number of significant digits.
In[1]:= N[Pi]
Out[1]=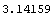 
This gives 
to 40 digits.
In[2]:= N[Pi, 40]
Out[2]=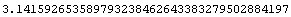 
Here is 
to 30 digits.
In[3]:= N[Sqrt[7], 30]
Out[3]=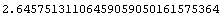 
Doing any kind of numerical calculation can introduce small roundoff errors into your results. When you increase the numerical precision, these errors typically become correspondingly smaller. Making sure that you get the same answer when you increase numerical precision is often a good way to check your results.
This is close to 7.
In[4]:= 2.6457 ^ 2
Out[4]=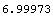 
The quantity 
turns out to be very close to an integer.
In[5]:= 262537412640768744 == N[ Exp[Pi Sqrt[163]] ]
Out[5]= 
To check that the result is not, in fact, an integer, you have to use sufficient numerical precision.
In[6]:= N[Exp[Pi Sqrt[163]], 50]
Out[6]= 
