5.2 Division of Integers
Division functions.
Range[n] gives the integers from 
to 
. Range is similar to Table.
In[1]:= r = Range[10]
Out[1]= 
This is a fast way to get the even numbers up to 
.
In[2]:= 2 r
Out[2]= 
Many functions work on whole lists.
In[3]:= EvenQ[r]
Out[3]=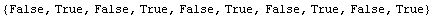 
You can also get the odd numbers.
In[4]:= 2 r - 1
Out[4]=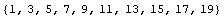 
The last three numbers are not odd integers.
In[5]:= OddQ[{2001, 2002, 3., 5 I}]
Out[5]=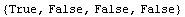 
This is the remainder on dividing 17 by 3.
In[6]:= Mod[17, 3]
Out[6]=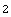 
This is the integer part of 
.
In[7]:= Quotient[17, 3]
Out[7]= 
This gives the same thing.
In[8]:= Floor[17 / 3]
Out[8]= 
Mod also works with real numbers.
In[9]:= Mod[5.6, 1.2]
Out[9]=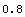 
If the division is exact, you get the quotient with the remainder zero.
In[10]:= {Quotient[4.8, 1.2], Mod[4.8, 1.2]}
Out[10]= 
The result from Mod always has the same sign as the second argument.
In[11]:= Mod[-5.6, 1.2]
Out[11]= 
For any integers a and b, it is always true that b * Quotient[a, b] + Mod[a, b] is equal to a.
