Numerical Calculations
You can do arithmetic with Mathematica TE just as you would on a calculator. You type the input 5 + 7; Mathematica TE prints the result 12.
In[1]:= 5 + 7
Out[1]=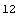 
Unlike a calculator, however, Mathematica TE can give you exact results. Here is the exact result for 
. The ^ is the Mathematica TE notation for raising to a power.
In[2]:= 3 ^ 100
Out[2]= 
You can use the Mathematica TE function N to get approximate numerical results. The % stands for the last result. The answer is given in scientific notation.
In[3]:= N[%]
Out[3]= 
You can find numerical results to any degree of precision. This calculates 
to 50 digits of precision.
In[4]:= N[ Sqrt[10], 50 ]
Out[4]=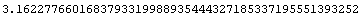 
Mathematica TE can evaluate all standard mathematical functions. Here is the value of the cosine function at 2.5.
In[5]:= Cos[2.5]
Out[5]=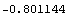 
Here is a root of 
near 
.
In[6]:= FindRoot[Sin[ 2^x ], {x, 2}]
Out[6]=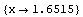 
You can calculate mathematical functions to any precision. This gives 
to 40 digits.
In[7]:= N[ Log[10, 13], 40 ]
Out[7]=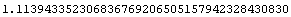 
Mathematica TE can do many kinds of exact computations with integers. The integer 70612139395722186 factors as 
.
In[8]:= FactorInteger[ 70612139395722186 ]
Out[8]=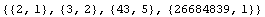 
Mathematica TE can also handle complex numbers. Here is 
. In Mathematica TE, I or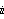 
stands for the imaginary number 
.
In[9]:= (3 + 4 I) ^ 10
Out[9]=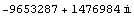 
You can find a local minimum of 
near 
. The function has a minimum, given by the first number, when 
takes the value to the right of the arrow.
In[10]:= FindMinimum[Sin[ 2^x ], {x, 2}]
Out[10]=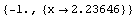 
You can do numerical integrals. Here is the numerical value of 
.
In[11]:= NIntegrate[ Sin[Sin[x]], {x, 0, Pi} ]
Out[11]= 
