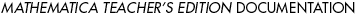
Applications in the sciences
Escape velocity and black holes
Introduction to the escape velocity
"Black holes are today an essential part of modern theoretical physics and astrophysics. Yet there are still some scientists (and many nonscientists) who find the notion of a black hole physically unacceptable. They believe the very idea is too outlandish to be real."--William Hiscock
Source: William A. Hiscock, "The Inevitability of Black Holes", Quantum 3(4), 1993, 26.
A black hole is a region of space where gravity is so intense that nothing, not even light, can escape. According to ordinary Newtonian physics as well as the Theory of Relativity, the escape velocity needed to escape the gravitational pull of a planet or star is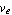 
, given by
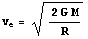
In this equation,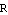 
denotes the radius of the planet or star, 
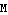denotes its mass, and 
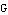is a universal gravitational constant. In Mathematica,we can use long names for variables, so we can write this as
If two bodies have the same radius but different masses, how do their escape velocities compare? A bigger mass will make a bigger square root. So, the bigger the mass, the bigger the escape velocity. If two bodies have the same mass but one has a larger radius than the other, how do their escape velocities compare? A bigger radius will make the fraction smaller, which will make the square root smaller. So, the bigger the radius, the smaller the escape velocity.
Escape velocity of the Earth
The radius of the Earth is about 6368 kilometers and its mass is about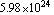 
kilograms. The universal gravitational constant is about 
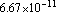. (The units are chosen so that the answer comes out in meters/second.) What is the escape velocity for Earth?
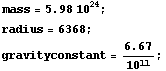
The escape velocity for Earth is in meters per second.
To convert this to miles per hour we load a Mathematica package.
Note: the command Needs["Miscellaneous`Units`"] loads a package in the Mathematica kernel that tells Mathematica how to do the unit conversion. If you attempt to use the Convert command without doing Needs["Miscellaneous`Units`"], the Convert command will not work.
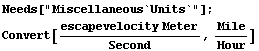
That is very fast! The velocity that a space shuttle needs to get into Earth orbit is only around 30,000 miles per hour. The escape velocity we found is for being able to "go off to infinity" beyond an Earth orbit.
How would you like to be a black hole?
Here is the equation for the escape velocity needed to escape ("to infinity") from a star or planet.
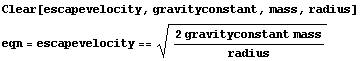
What happens if we take a body of fixed mass and make it smaller in size? The radius will get smaller so the escape velocity will get bigger. What if we take that body of fixed mass and squash it so that its radius is really tiny? Is there any limit to how large we can make the escape velocity? Mathematically, there is no limit to how big we can make the escape velocity; just keep making the radius smaller and smaller.
According to the best evidence we have, nothing in the universe can go faster than the speed of light. If we make that radius too small, then the escape velocity becomes greater than light speed--that is, not even light itself can escape. That means we have a black hole.
Here's the equation again.
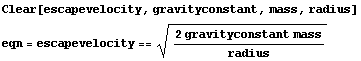
We can solve this equation for the radius.
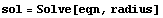
The radius you get when you take the escape velocity to be the speed of light is called the Schwarzschild Radius. The speed of light is about 3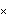
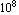(meters/second), and the universal gravitational constant is about 6.67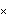
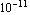(in units that are appropriate). This gives:
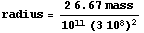
(If the mass is expressed in kilograms, then the radius is given in meters.)
Earth has a mass of about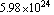 
kilograms. So, Earth's Schwarzschild radius is about
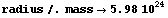
That is about 0.01 meters, or about one centimeter. Squash the entire Earth into a centimeter-sized ball and you have a black hole.
U.S. population trends
Here are some data on the U.S. population based on the census that is done every 10 years.
Source: "U.S. Population by Official Census 1790-1990", in The World Almanac and Book of Facts 1998, Mahwah, NJ: World Almanac Books, 1997, 380-381.
Here are two exercises together with their solutions.
Make one plot for the population for the years 1790 to 1890, and another plot for the years 1900 to 1990. What differences show up between the two plots?
Here are the data for the years 1790 to 1890.
Tip: We just copied and pasted part of uspop from the preceding data.
Here is the plot of the data for the early years.
Here are the data for the years from 1900 to 1990.
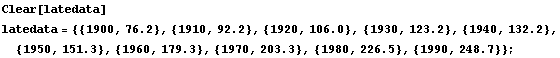
Here is the plot of the data for the later years.
Here is the plot of both of them together.
It looks like steady growth on both plots. In the later years, it looks like if you connect the dots you get something like a line. We say the graph looks like a linear plot. The important thing here is that the growth rate, or slope, remains constant.
On the other hand, in the early years it looks more like you get a function whose growth rate goes up as time goes on. If you connect the dots you get a curve that looks like an exponential function, and we say the graph looks like an exponential plot.
For more details on this, look at the sections and .
This may be a little surprising, since the growth actually has been steeper in the later years. Here are the average rates of growth for the two times separately.
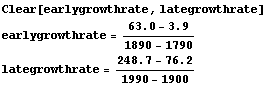
The growth rate in the later years is more than three times what it was in the early years.
Make a table of the change in population from census to census and plot those changes. Describe what you see.
Here are the original population data again.
Source: "U.S. Population by Official Census 1790-1990", in The World Almanac and Book of Facts 1998, Mahwah, NJ: World Almanac Books, 1997, 380-381.
Here is a table of the changes.
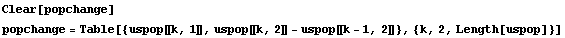
The points are of the form {census year, change since last census}.
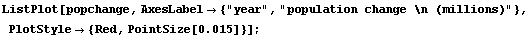
There are a few periods when the population change went down. (Does that mean that the population went down? No, it does not; look back at the original population data.)
What were those periods when the population change went down? What was going on in the country or the world that might have influenced the population change here?
The population change was always positive; that says that the population always was going up. If the population change was smaller but still positive, that just says the population was growing at a slower rate.
The population change slowed during the periods 1860-1870, 1910-1920, and 1930-1940. These periods included the U.S. Civil War, World War I, and the Great Depression, respectively. The population growth has also been on a slow but steady decline since 1960.
Interest rates
According to a story by the Associated Press, the Russian ruble drastically fell in value against the U.S. dollar in October 1994. The Russian government decided--among other actions--to raise short-term interest rates--from 130 percent to 170 percent.
Source: "Ruble's plunge spreads panic in Moscow", Louisville Courier-Journal, 12 Oct. 1994.
"Low" interest: 130 percent
Suppose you had $1500 that you could deposit in a bank at an annual simple interest rate of 130%. How would your earnings increase if you left it there for 10 or 15 years?
This is compound interest. And that is 130%; as a decimal,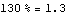 
, not .013, which is the decimal form of 1.3%! No matter what balance you have at the end of one year, at the end of the next year you will have 130% of that balance added on in interest. Let's call balance[yr] the amount you have at the end of year yr. Then we have:
We also know that
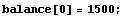
That is enough to let us find out what the balance will be any time in the future.
Here is a plot.
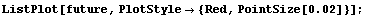
We see very large numbers. After 10 years, you would have
dollars, which is about $6 million. After 15 years, you would have
dollars, which is just under $400 million. Not bad (if you did not have to worry about prices of everything going up also).
