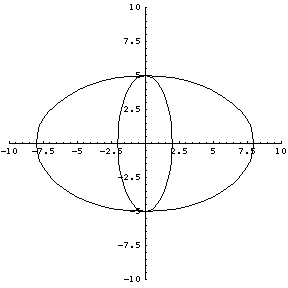
Conic Sections: Ellipses
Student Name:
Definition of an Ellipse
Horizontal Ellipses (Major Axis Is the x-Axis)
An ellipse is simply an oval, where both ends are the same.
The standard form of the equation of an ellipse with center at (0, 0) is
.
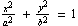This is an ellipse with a major axis (the longest dimension) along the x-axis and the minor axis (the shortest dimension) along the y-axis. This produces an oval that is longest on the x-axis, or horizontal.
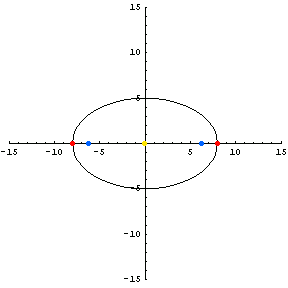
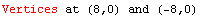
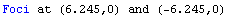
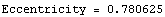
Notice that several points are labeled along the major axis.
It is also important to know about the following.
Vertical Ellipses (Major Axis Is the y-Axis)
When the ellipse is rotated 90 degrees, the major axis is now the y-axis. The standard form of the equation of an ellipse with the major axis on the y-axis and a center at (0, 0) is
.
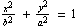Notice that the only difference between the two types of ellipses is the arrangement of the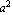 
and 
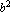terms. Since a is the distance from the center to the ellipse along the x-axis and b is the distance from the center to the ellipse along the y-axis, you can easily tell the orientation of the ellipse by looking at which term is larger.
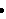If a is larger, then it is placed under the 
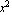term, and the major axis will be the x-axis.
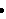If b is larger, then it is placed under the 
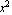term, and the major axis will be the y-axis.
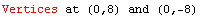
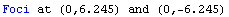
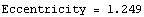
Eccentricity-A Measure of Flatness
The eccentricity of an ellipse tells us about the flatness of an ellipse.
Notice that the eccentricity of the first example (a horizontal ellipse) is 0.780. The eccentricity of the second example (a vertical ellipse) is 1.249.
This measurement is calculated by the following formulas:
calculating c, where 
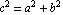
eccentricity =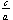 
For any horizontal ellipse, the "shorter" the shape of the ellipse, the closer the eccentricity will be to one. The taller the horizontal ellipse, the closer the eccentricity will be to zero.
For any vertical ellipse, the "taller" the shape of the ellipse, the larger the eccentricity will be. Keep in mind, however, that the eccentricity of any ellipse will never be larger than the b term, since this is the true "height" of the ellipse.
For both types of ellipses, the more the ellipse looks like a circle, the closer the eccentricity will be to zero.
Practice Problems
Problem 1: The Orbit of the Earth
The orbit of the Earth around the sun is elliptical. The length of the major axis (a) is186 million miles. The length of the minor axis (b) is 185.972 million miles.
Graph the ellipse of the Earth's orbit, scaling your number by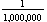 
.
Hint: Keep in mind that the length of the major and minor axes from one endpoint to the other, not from the endpoint to the center of the ellipse.
Problem 1 Answers:
The Sun is at one foci of this ellipse. What is the shortest distance between the Earth and the Sun?
What is the largest distance between the Earth and the Sun?
Describe the shape of the orbit of the Earth around the Sun in terms of its eccentricity.
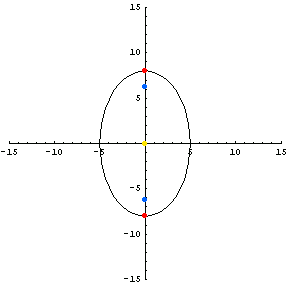
Problem 2: Comparing Two Ellipses
Two ellipses have been drawn in the graph below. Use the graph to answer the following questions:
1. What is a in the larger ellipse?
What is b in the larger ellipse?
What is the length of the major axis of the larger ellipse?
2. What is a in the smaller ellipse?
What is b in the smaller ellipse?
What is the length of the major axis of the smaller ellipse?
3. Describe how the eccentricity measurements would differ between the two ellipses.
