8.7 Similarity Transformation

There can be an infinite number of realizations of a physical system that correspond to the system's representations in different bases of state space. The transformation from basis to another basis, , may be performed with any nonsingular matrix . In the new basis, the state equations from Eq. (8.1) become

where

The result can be obtained using the function SimilarityTransform.

Finding the similarity transformation.

Consider an earlier system.

In[33]:=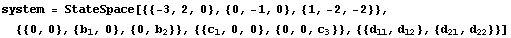

Out[33]=

Here its eigenvectors are arranged as columns of the matrix.

In[34]:=

Out[34]=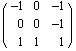

A similarity transformation based on the inverse of that matrix can be used to represent the system in its canonical form.

In[35]:=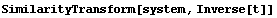

Out[35]=

To avoid a double inversion of the matrix in Eq. (8.5), either or its inverse can be supplied as an input argument to SimilarityTransform. In the latter case, the option InvertedTransformMatrix must be set to True. Another way to look at this option is that it allows backward transformation from basis to .

This performs the transformation, assuming that matrix t is the inverse of the transformation matrix.

In[36]:=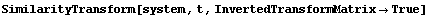

Out[36]=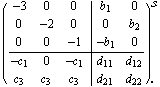

Further performance gain can be achieved if the transformation matrix is known to be orthogonal, in which case the transpose of the matrix can be used instead of its inverse.

Options to SimilarityTransform.