|
3.5.2 ACEquations

Command structure of ACEquations.
Given a Transient or DC DAEObject, ACEquations linearizes the equation system about the given operating point oppoint and returns an AC DAEObject. The operating point is given by a list of rules of the form var -> value for each variable of the equation system. It is possible to assign values to time derivatives of variables, too. The list of value mappings is added to the DesignPoint option of the returned DAEObject. During linearization, the values of AC sources are replaced by their AC value as given by sources, where sources is a list of rules of the form acsource -> val for each parameter representing an AC source. If this third argument is omitted, the AC values are automatically extracted from the ModeValues option stored in the DAEObject.
Note that, given a Netlist or Circuit object, you can set up AC equations directly using CircuitEquations.
ACEquations provides the following options:

Options for ACEquations.
See also: DCEquations, CircuitEquations.
Options Description
A detailed description of all ACEquations options is given below in alphabetical order:
DerivativePostfix
If symbol names denoting derivates of varibles have to be created during linearization, the value of the DerivativePostfix option is appended to the variable name. Thus, the value of the DerivativePostfix option has to be a string which can be converted to a valid Mathematica symbol. The default setting is DerivativePostfix -> "d".
FrequencyVariable
The option FrequencyVariable specifies the symbol denoting the complex Laplace frequency. If set to Automatic, the value of the option FrequencyVariable as stored in the DAEObject dae is used. The default setting is FrequencyVariable -> Automatic.
OperatingPointPostfix
If the given operating point list oppoint contains a rule of the form var -> value, the rule opvar -> value is added to the DesignPoint option of the returned DAEObject, where opvar is given by appending the value of the OperatingPointPostfix option to the variable name var. Thus, the value of the OperatingPointPostfix option has to be a string which can be converted to a valid Mathematica symbol. The default setting is OperatingPointPostfix -> "$op".
Examples
Load Analog Insydes.
In[1]:= <<AnalogInsydes`
Define netlist description of a simple diode rectifier circuit.
In[2]:= rectifier = Circuit[
Netlist[
{V0, {1, 0}, Symbolic -> V0,
Value ->2. Sin[10^6 Time]},
{R1, {2, 0}, Symbolic -> R1, Value -> 100.},
{C1, {2, 0}, Symbolic -> C1, Value -> 1.*^-7},
{D1, {1 -> A, 2 -> C},
Model -> "Diode", Selector -> "Spice",
GMIN -> 0, AREA -> 1}
]
]
Out[2]= 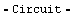
Set up transient equation system.
In[3]:= tran = CircuitEquations[rectifier,
ElementValues -> Symbolic,
AnalysisMode -> Transient,
Value -> {"*" -> {TEMP, TNOM, $q, $k, AREA, GMIN}}]
Out[3]= 
Show equation system.
In[4]:= tran // DisplayForm
Out[4]//DisplayForm= 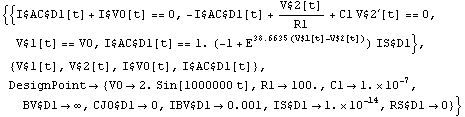
Calculate operating point.
In[5]:= op = First[NDAESolve[tran, {t, 0.}]]
Out[5]= 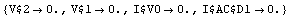
Linearize equations about the operating point.
In[6]:= ac = ACEquations[tran, op, {V0 -> 1}]
Out[6]= 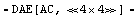
Extract equation system.
In[7]:= GetEquations[ac]
Out[7]= 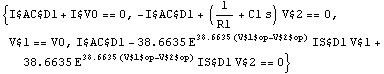
Display design point stored in the DAEObject. Note that new parameters have been generated.
In[8]:= GetDesignPoint[ac]
Out[8]= 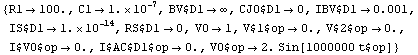
|