11.1.4 Four-Bar Example Mechanism

To demonstrate the use of generalized coordinate constraints in a Modeler2D model, a 2D model of a simple four-bar mechanism is developed. The model consists of three moving bars and one stationary bar, the ground. This same model is also used in Section 8.3 and Chapter 9, so it is presented very briefly here.

This loads the Modeler2D packages.

In[12]:=

Here is the four-bar mechanism, shown with the locus of a moving point.

Bodies

Four body objects are required for the four-bar model. Each bar is attached to another bar at its local origin and at a point at the other end of the bar on the local X or Y axis.

Here are the body objects for the four-bar model.

In[16]:=

The body properties are incorporated into the model.

In[20]:=

Constraints

Five constraints, one of which is a driving constraint, are used to model the four-bar mechanism. These constraints are simply standard Mech constraints that will be replaced with generalized coordinate constraints shortly.

Here are the constraint objects for the four-bar.

In[21]:=

The constraints are incorporated into the current model.

In[26]:=

Runtime

Because of the presence of T in the driving constraint cs[1], the model can be run through its intended range of motion by varying T directly with the SolveMech command. The numerical value of T specifies the angle of rotation of the drive bar in revolutions.

The model is run at T = 0.3.

In[27]:=

Out[27]=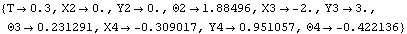

Here is the four-bar model at T = 0.3.

Generalized Coordinate Constraints

Now one of the standard constraints is replaced with a generalized coordinate constraint. Constraint 2, the revolute joint at the drive bar origin, is replaced first, and body 2 becomes a slave to the ground body, represented by the single coordinate alpha.

Here is the new constraint.

In[28]:=

The modified model is run again at T = 0.3.

In[30]:=

Out[30]=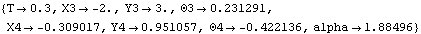

Note that the symbols X2, Y2, and 2 are no longer included in the solution rules returned by SolveMech. The location of body 2 is represented entirely by alpha, which has the same numerical value as 2 used to have. The numerical value of alpha would be different from 2 if the direction vectors of the two axes in the GenRevolute2 constraint were not identical (X and X).
Two more of the Revolute2 constraints can also be replaced, but not the fourth one. This is because each generalized coordinate constraint creates a slave body, and a slave body can be a slave to only one master body. Thus, there is no way to use four generalized coordinate constraints in a model with only three bodies. Any three of the four revolute constraints can be replaced, but not all of them.

Here are two more new constraints.

In[31]:=

In[32]:=

In[33]:=

The modified model is run again at T = 0.3.

In[34]:=

Out[34]=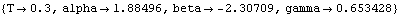

Now all of the Cartesian coordinates have been replaced with the generalized coordinates alpha, beta, and gamma. A quick degree of freedom count shows that this all makes sense: the three generalized coordinate constraints each add one degree of freedom to the model, while the two standard constraints Revolute2 and RotationLock1 constrain a total of three degrees of freedom.
The physical meaning of the new coordinates is quite clear: alpha is the angle between the X axis of the ground and the local x axis of the drive bar, beta is the angle between the local x axes of the drive and center bars, and gamma is the angle between the local x axes of the center and driven bars.

Output and Graphics Functions

Now that we have a solution in terms of the generalized coordinates, all of the standard Mech output and graphics functions allow it to be used in the same manner as a solution in Cartesian coordinates. For example, the location of a point is still found with the Location function and the rotation angle of a body is found with Rotation. The symbolic expressions returned by these functions reflect the new coordinate system being used, but the numerical results are equivalent.

Here are the Cartesian coordinates of point 2 on the center bar.

In[35]:=

Out[35]=

Out[36]=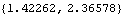

Here is the global rotation angle of the driven bar. Note that it is numerically equal to the 3 coordinate from the first set of solution rules.

In[37]:=

Out[37]=

Out[38]=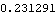

The location of point 2 on the center bar is a function of alpha and beta, but not gamma. This is because of the master-slave relationship of the generalized coordinate bodies; the center bar is a slave to the drive bar, which is a slave to the ground. Thus, the location of any point on the driven bar is a function of all three generalized coordinates, and the location of any point on the drive bar is a function of only alpha.
Mech graphics functions also operate without regard to the use of generalized coordinates. The following graphics object will generate the same image with any of the three constraint formulations used previously.

Here is the graphics object representing the four-bar model.

In[39]:=

This shows the graphic at T = 0.45.

In[40]:=

Out[40]=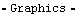