11.2 Loads and ReactionsThis section deals with issues related to applying loads to mechanisms modeled with generalized coordinates, and finding the reaction forces associated with those coordinates. 11.2.1 Applied LoadsUsing generalized coordinates has almost no effect on the modeling of applied loads. The standard Mech load functions Force, Moment, Gravity, and GyroMoment are used to apply loads to a generalized coordinate slave body in exactly the same way as they are used with standard bodies. The one load function that is affected by the use of generalized coordinates is Load, which is used to apply a load directly to a specified coordinate.
Since Load references the coordinates in a model directly by their symbolic name, it can be used to apply a load directly to a generalized coordinate. Conversely, Load cannot be used to apply a load directly to a Cartesian coordinate of a slave body because a slave body doesn't have any explicit Cartesian coordinates.
For example, suppose a model has two bodies, 2 and 3, and body 3 is a slave to body 2. The two bodies are joined by a revolute joint and the symbol alpha represents the rotation of the slave, relative to the master. The Force function may be used to apply a force in the global X direction to the slave, but the Load function may not. This loads the Modeler2D packages and defines names for bodies 2 and 3. Here is a load object that applies a 10-unit force to the slave body.
Out[4]= |  |
This load object does not apply the 10-unit force to the slave body, because X3 is not a coordinate in the model.
Out[5]= |  |
However, the Load function can be used to apply a moment to the slave body because the generalized coordinate alpha is an angular coordinate. A load applied directly to alpha essentially applies a counterclockwise moment to the slave body, and a clockwise moment to the master. Here is a load object that applies a 10-unit moment to the slave, and an equal and opposite moment to the master.
Out[6]= |  |
Here is a simpler load object that applies the same 10-unit couple between the slave and master.
Out[7]= |  |
In general, the Load function should be used instead of Force or Moment whenever possible because the resulting algebraic expressions that are added to the model can be much simpler. 11.2.2 Constraint ReactionsWhile the use of generalized coordinates has little effect on the application of loads to a model, finding constraint reaction forces is another matter. When a constraint is eliminated from a model by using generalized coordinates, information regarding the reaction forces at the constraint is lost. This is one basic disadvantage of a reduced coordinate system; by algebraically eliminating coordinates from a model we lose information about those coordinates.
Thus, three restrictions are placed on models using generalized coordinates: the Reaction function cannot be used to find the reaction forces applied by a generalized coordinate constraint to any body (because it is not really a constraint), the Reaction function cannot be used to find the reaction forces applied by any constraint to a generalized coordinate slave body (because the body doesn't have Cartesian coordinates), and the Loads function cannot be used to find the loads applied to a slave body (for the same reason).
Both the Reaction and Loads functions may still be used with generalized coordinates, but they must be used to access the coordinates directly.

Alternate usages of Reaction and Loads. The physical meaning of the quantities returned by Reaction and Loads is quite clear, in the context of the simple generalized coordinate constraints. If the generalized coordinate sym represents an angle in radians, then the loads on the coordinate are in consistent units of moment. If the coordinate sym represents a distance, then the loads on the coordinate are in consistent units of force.
However, if abstract user-defined generalized coordinate constraints are used, the generalized loads may have little physical meaning, just like the generalized loads associated with each constraint (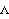 1, 1, 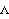 2, ...) sometimes have little physical meaning. The one meaning that always applies to a generalized load is this: a generalized load multiplied by a small variation in its associated generalized coordinate is equal to a small variation in work, in consistent energy units. 2, ...) sometimes have little physical meaning. The one meaning that always applies to a generalized load is this: a generalized load multiplied by a small variation in its associated generalized coordinate is equal to a small variation in work, in consistent energy units. 11.2.3 Slider-Crank Example MechanismTo demonstrate the use of the Reaction and Loads functions with generalized coordinates a planar model of a simple slider-crank mechanism is developed. This model uses only two bodies, the slider and crank, and it is modeled with two generalized coordinates, the rotation angle of the crank and the X displacement of the slider. This loads the Modeler2D packages and defines some useful constants. Here is the slider-crank mechanism.

Bodies Two body objects are defined for the slider-crank model. Inertia properties are defined for each moving body so that the dynamic reaction forces can be calculated. No local point definitions are made in the body objects. All necessary point coordinates in this model are given explicitly in the constraint functions. Here are the body objects for the slider-crank model. The body properties are incorporated into the model. ConstraintsFour constraints are used to model the slider-crank mechanism. Two generalized coordinate constraints are used along with two standard constraints. A GenRevolute2 constraint defines the symbol alpha as the angular coordinate of the crank.A RotationLock1 constraint controls the rotation of the crank.A GenTranslate2 constraint defines the symbol beta as the displacement coordinate of the slider.A RelativeDistance1 constraint models the connecting rod between the crank and the slider.Here are the constraint objects for the slider-crank mechanism. The constraints are incorporated into the current model. LoadsA force that is a linear function of slider position is applied to the slider to simulate a simple spring. The spring has a spring constant of 10, and it is placed so that the spring force is zero when the X displacement of the slider is three units. Here is a spring force applied to the slider. The model is run at T = 0.1 with the Static option to cause the Lagrange multipliers to be calculated.
Out[22]= |  |
ReactionsBecause generalized coordinates were used in this model, Mech's ability to find constraint reaction forces is limited. Normally, Reaction could be used to find the reaction force vector that the revolute joint applies to the crank, but with this model only the moment applied to the crank by constraint 2 can be found. Note that Reaction cannot directly find the moment applied to body 2, it can only find the generalized force associated with the symbol alpha. Since alpha is an angular coordinate, its associated load is a moment. Here is the moment applied to the crank by the driving constraint.
Out[23]= |  |
Of course constraint 4, the RelativeDistance1 constraint, applies an equal and opposite moment to the crank. Here is the moment applied to the crank by the connecting rod.
Out[24]= |  |
Out[25]= |  |
Constraint 4 also applies a reaction force to the slider. Again, the restraining force and torque that would be applied to the slider by a normal Translate2 constraint cannot be found. Only the generalized force associated with beta can be found, which is the X direction force on the slider. Here is the force applied to the slider by the connecting rod.
Out[26]= |  |
Here are the external loads applied to the coordinates alpha and beta.
Out[27]= |  |
The inertia terms are automatically converted into the proper coordinate system so that the dynamic reaction forces may be calculated. The Solution -> Dynamic option causes SolveMech to include the inertial loads and calculate the reaction forces. Here is a plot of the torque required to drive the crank through a full cycle.

Out[28]= |  |
Here is the graphics function that generates the image of the slider-crank mechanism. Here is the slider-crank mechanism at T = 0.35.

Out[30]= |  |
|