2.3 Constraint ObjectsConstraint objects are used to define the mathematical relationships that make up the kinematic model in terms of the physical relationships of the various mechanism bodies. All Mech constraint functions return constraint objects with the head SysCon. These constraint objects are passed to the SetConstraints function to build the mathematical model. 2.3.1 General FormatAll arguments to any constraint function follow the same general format. Format for all constraint functions. Further, all constraint function names end with a single digit, except the general constraint function Constraint. This digit signifies the number of degrees of freedom constrained by the constraint. For example, the 2 in the Translate2 constraint function name signifies that it contains two constraint equations and constrains two degrees of freedom in a model. 2.3.2 2D Basic ConstraintsThe Modeler2D basic constraints specify elementary geometric relationships between points and lines on mechanism bodies. Elementary relationships are used for the majority of simple mechanical joints. A shaft spinning in a bearing is modeled by specifying that two points are coincident. A connecting rod can be modeled by specifying a constant distance between two points. A guide pin in a slot is modeled by specifying that a point on one body lies on a line on another body. A piston in a cylinder is modeled by specifying that two lines on two different bodies are colinear.
Many seemingly different mechanical joints are often modeled with the same constraint, such as a connecting rod versus a guide pin in a circular track; both are modeled by specifying the distance between two points on two different bodies. It is up to the user to determine the true nature of the kinematic relationships that make up a mechanism.
The entire set of Modeler2D constraint functions is quite redundant; all basic 2D mechanisms could, in fact, be modeled with a small subset of the Modeler2D constraints. The goal in this is to provide a constraint that is similar in form to the actual mechanical joint being modeled. Thus, the readability of the model can be improved.

Local coordinate constraints directly control the local coordinates of specified bodies. Point-on-line constraints force a point on a body to travel along a specified line. Point-at-position constraints force a point on a body to lie at a specified position. Angular constraints control the angle between the direction vectors of two lines. Compound constraints enforce multiple geometric relationships simultaneously. There are several other compound constraints available for modeling gears and cams, these are discussed in Chapter 6.
To demonstrate the ambiguity in determining which constraint is the correct constraint, the set of four constraints used in the crankshaft-piston model are examined. The first constraint, Revolute2, could be modeled with a pair of constraints with one degree of freedom each; a RelativeX1 to control the X coordinate of the crankshaft axis, and a RelativeY1 to control the Y coordinate. This loads the Modeler2D package. The Revolute2 constraint is functionally identical to a pair of one degree of freedom constraints. The second constraint, RotationLock1, could be modeled by constraining the angle between two lines, one on the crankshaft and one on the ground. Here are two equivalent constraints. The RelativeDistance1 constraint, in this application, cannot be replaced by the use of any other constraint. It is somewhat unique, geometrically. This constraint has no functional equivalent. 2.3.3 3D Basic ConstraintsThe Modeler3D basic constraints specify elementary geometric relationships between points, lines, and planes on mechanism bodies. Elementary relationships are used for the majority of mechanical joints. A shaft spinning in a bearing is modeled by specifying that two axes are coincident. A connecting rod can be modeled by specifying a constant distance between two points. A guide pin in a slot is modeled by specifying that a point on one body lies on a line on another body. A piston in a cylinder is modeled by specifying that two lines on two different bodies are colinear.
Many seemingly different mechanical joints are often modeled with the same constraint, such as a connecting rod versus a guide pin in a circular track; both are modeled by specifying the distance between two points on two different bodies. It is up to the user to determine the true nature of the kinematic relationships that make up a mechanism.
The entire set of Modeler3D constraint functions is quite redundant; all basic 3D mechanisms could, in fact, be modeled with a small subset of Modeler3D constraints. The goal in this is to provide a constraint that is similar in form to the actual mechanical joint being modeled. Thus, the readability of the model is improved.

Local coordinate constraints directly control the local coordinates of specified bodies. Point-on-surface constraints force a point to lie on a specified surface. Point-on-line constraints force a point to lie on a line or curve. Point-at-position constraints control the position of a point. Angular constraints control the angle between two vectors. Parallel constraint enforces parallelism between two vectors. Constraints that enforce more complex geometric relationships. Compound constraints enforce multiple geometric relationships simultaneously. There are several other compound constraints available for modeling gears and cams; these are discussed in Chapter 6.
To demonstrate the ambiguity in determining which constraint is the correct constraint, the set of five constraints used in the crankshaft-piston model are reexamined. The first constraint, a Revolute5, could be modeled instead with two constraints; a Spherical3 constraint to control the position of the crankshaft, and a Parallel2 constraint to control the direction vector of the crankshaft's axis. This loads the Modeler3D package. Here is the original Revolute5 constraint. Here are an alternative pair of constraints that are functionally equivalent to the Revolute5 constraint. The third constraint, Cylindrical4, could be modeled by using two PointOnLine2 constraints. Here is the original Cylindrical4 constraint. Here are two constraints that are equivalent to the Cylindrical4 constraint. The RelativeDistance1 constraint in this application cannot be replaced by the use of any other constraint. It is somewhat unique, geometrically. This constraint has no functional equivalent. 2.3.4 The General ConstraintThe general constraint allows the user to enter a mathematical relationship directly as an equation. The general constraint function. For example, to constrain the origin of body 2 to lie on a paraboloid surface in the global coordinate system with its axis in the Z direction and Z intercept at {0, 0, 4}, Constraint would be used as follows. Here is a general mathematical constraint.
Out[22]= | 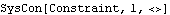 |
|