Mechanical Systems / Output Functions / 3D Output Functions /
Previous section-----Next section

3.2 3D Output Functions

Numerical output from a Modeler3D model can be generated with output functions that are defined in the auxiliary package Graphics3D. This package is autoloaded after the Modeler3D main package has been loaded if any of the output functions are called. Each output function returns a symbolic expression that represents the quantity being sought, in terms of the model's dependent variables X2, Z3, Ei4, and so on. To achieve a numerical result, the dependent variables must be replaced with numbers, typically by applying a solution rule returned by SolveMech. More complicated and specific output functions can easily be defined by the user, making use of Mech's basic output functions and Mathematica's built-in vector algebra functions.

3.2.1 Example Mechanism

To demonstrate the use of Modeler3D output functions, a 3D model is developed that can be measured. The model is a spatial slider-crank mechanism consisting of two moving bodies, the crank and the slider. A real slider-crank mechanism would have a fourth body, the connecting rod between the crank and the slider.
The motion of the slider-crank mechanism is driven by the rotation of the crank, which forces the slider to reciprocate in a straight track that is parallel to the axis of the crank. The crank is attached to the slider via a connecting rod that is modeled by a distance constraint.

This loads the Modeler3D package.

In[1]:=

Here is a graphic of the complete 3D slider-crank model.

Bodies

Three body objects are defined for the slider-crank mechanism model. Note that the zeroth point is used in this model to avoid repeatedly defining a point at coordinates {0, 0, 0}.

  • The ground (body 1) has four points defined in its body object.
    P1 and P2 are two points to define the rotational axis of the crank.
    P3 and P4 are two points that are used in conjunction with the origin of the ground body to define the translation axis and reference direction of the slider. P4 is also used with the local origin to define a reference direction for the crank's rotation.
  • The crank (body 2) has two points defined in its body object.
    P1 is a point that is used with the crank's local origin to define its rotational axis.
    P2 is the attachment point of the connecting rod, and also a reference for the crank's rotation.
  • The slider (body 3) has two points defined in its body object.
    P0 is the attachment point of the connecting rod on the slider.
    P1 is used with the slider's local origin to define its translation axis.
    P2 is used with the slider's local origin to define a reference direction for the translational joint.

    • Here are all the bodies in the slider-crank model.

    Here are names for each of the body numbers in the model.

    In[2]:=

    Here are body objects for each body.

    In[5]:=

    This incorporates the body properties into the current model.

    In[8]:=

    Constraints

    Four constraints are used to model the slider-crank mechanism.

  • A Revolute5 constraint forces the axis of the crank to be coincident with its pivot axis on the ground. This leaves only one degree of freedom for the crank, rotation about its axis.
  • A ProjectedAngle1 constraint specifies the angular relationship between a line on the ground body and a line on the crank. This driving constraint is used to rotate the crank.
  • A RelativeDistance1 constraint between the crank and the slider replaces the pseudo-connecting rod, which is 30 units long.
  • A Translate5 constraint between the slider and the ground leaves only one degree of freedom for the slider; horizontal translation along a track on the ground body. This constraint references two Modeler3D Axis objects that are constrained to be parallel and coincident, and the reference directions of the two axes are constrained to be coplanar.

    • Here are the constraints for the slider-crank model.

    In[9]:=

    This incorporates the constraints into the current model.

    In[13]:=

    Runtime

    Now run the model at T = 0.05.

    In[14]:=
    Out[14]=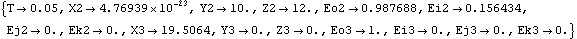

    Here is the slider-crank model at T = 0.05.

    3.2.2 Output Functions

    Modeler3D numerical output functions return expressions that evaluate to numbers or vectors, such as the distance between two points, the angle between two lines, or the coordinates of a point. These functions take Modeler3D point, vector, and axis objects as arguments, identical in structure to the geometry objects used when building constraints. When local point numbers are used, the local coordinates are taken from the current body objects, as specified with SetBodies.
    Each of the output functions is demonstrated in the context of the quick-return mechanism model defined in Section     3.2.1.

    Output functions.

    More output functions.

    The Location function is used to convert a Mech point object into the global coordinates of the point.

    Here are the global coordinates of the attachment point of the connecting rod on the crank.

    In[15]:=
    Out[15]=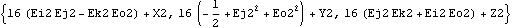

    Location assumes a point object if only the arguments of Point are given.

    In[16]:=
    Out[16]=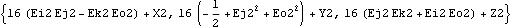

    Now get a numerical result.

    In[17]:=
    Out[17]=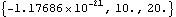
    Out[18]=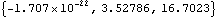

    The Distance function is used to find the absolute distance between any two points in space. The two points can be on one body or two different bodies.

    Here is the distance from a point on the axis of the crank to the origin of the slider.

    In[19]:=
    Out[19]=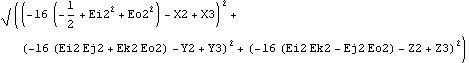

    Now get a numerical result.

    In[20]:=
    Out[20]=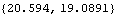

    Here is the length of the line from the center of the crank to the drive pin.

    In[21]:=
    Out[21]=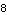

    Note that it was not necessary to apply a solution rule to the last example to get a numerical result because the dimension that was measured was a constant.

    Here is the minimum distance between the crank axis and the center line of the connecting rod.

    In[22]:=
    Out[22]=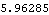

    Here is the angle between the connecting rod and the crank axis.

    In[23]:=
    Out[23]=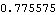

    Now convert the previous result to degrees.

    In[24]:=
    Out[24]=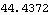

    The measure of an angle in 3D space requires a reference frame for measurement. ProjectedAngle allows the plane of projection of the angle to be specified.

    Here is the angle of a line on the crank, relative to a line on the ground, as viewed looking down the crank axis.

    In[25]:=
    Out[25]=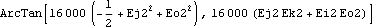

    Now get a numerical result at T = 0.35.

    In[26]:=
    Out[26]=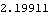

    This angle should be equal to 35/100 of a turn, since that is what we have specified with SolveMech.

    In[27]:=
    Out[27]=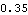

    This finds the intersection of the connecting rod axis and a horizontal plane through the crank axis.

    In[28]:=
    Out[28]=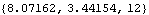

    The angular orientation of a body in 3D space can be uniquely specified by a single rotation about a fixed axis. Rotation returns the angle and axis associated with the current spatial orientation of a body. See Section 4.2 for more examples on the angular orientation of 3D bodies.

    This finds the angle and axis of rotation of the crank.

    In[29]:=
    Out[29]=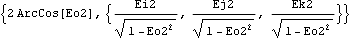

    Now get a numerical result.

    In[30]:=
    Out[30]=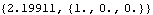

    3.2.3 Vector Algebra Functions

    Modeler3D vector algebra functions perform many common vector algebra operations, such as cross and dot products of vectors. These functions can be used to build more complicated functions that are not provided by Modeler3D. These functions take point, vector, and axis objects as arguments, just like the output functions described in Section 3.2.2. When local point numbers are used, the local coordinates are taken from the current body objects, as specified with SetBodies.
    Each of the vector algebra functions is demonstrated in the context of the slider-crank mechanism model defined at the beginning of this section.

    Vector algebra functions.

    The Direction function is used to convert Modeler3D vector objects into 3D vectors in global coordinates.

    Here is the direction vector of the connecting rod.

    In[31]:=
    Out[31]=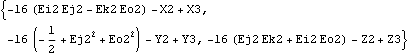

    Now get a numerical result.

    In[32]:=
    Out[32]=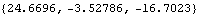

    Several Modeler3D output functions are textbook vector algebra functions that are capable of dealing with normal 3D vectors or Modeler3D vector/axis objects interchangeably.

    Magnitude can return the length of the line from one end of the connecting rod to the other.

    In[33]:=
    Out[33]=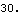

    Here is the length of a simple 3D vector.

    In[34]:=
    Out[34]=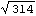

    Unit also works with vectors or vector objects.

    In[35]:=
    Out[35]=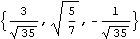

    The cross product of two vectors is found with the Cross function.

    Here is the cross product of a Modeler3D Line object and a vector.

    In[36]:=
    Out[36]=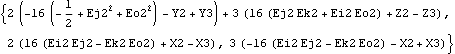

    Now get a numerical result.

    In[37]:=
    Out[37]=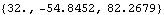

    Here is the 3D rotation matrix associated with the crank.

    In[38]:=
    Out[38]=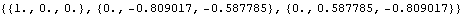

    Here is the skew symmetric matrix operator.

    In[39]:=
    Out[39]=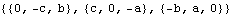

    The global coordinates of a point specified in a local reference frame are equal to the coordinates of the origin of the reference frame plus the local coordinates of the point, rotated into the global reference frame.

    Here is a calculation of the global coordinates of the local point {3, 8} on the slider.

    In[40]:=
    Out[40]=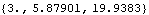

    The Location function performs effectively the same calculation.

    In[41]:=
    Out[41]=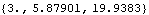

    The PointToLocal function converts the global point back to local coordinates.

    In[42]:=
    Out[42]=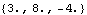

    A constant utility.

    Coordinate Conversions

    The following four conversion functions will not accept Modeler3D geometry objects as arguments. These functions only accept 3D vectors of the form {x, y, z}.

    Coordinate conversions.

    Coordinate conversion options.

    This converts a cylindrical coordinate triplet to Cartesian coordinates.

    In[43]:=
    Out[43]=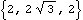

    This converts it back.

    In[44]:=
    Out[44]=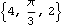

    This converts a 3D vector to polar coordinates.

    In[45]:=
    Out[45]=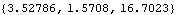